Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 28
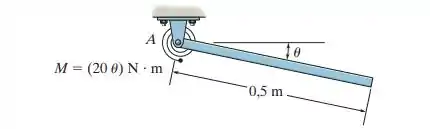
Uma mola de torção linear deforma-se de modo que um momento de binário nela aplicado esteja relacionado a sua rotação em radianos pela equação . Se essa mola estiver presa à extremidade de uma haste uniforme de 10 kg conectada por um pino, determine o ângulo para que haja equilíbrio. A mola não está deformada quando .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar o ângulo para que o mecanismo dado na questão esteja em equilíbrio. E se estamos falando de equilíbrio, temos que lembrar das seguintes equações:
Apesar de aparentar ser difícil, esta é uma questão bem fácil. Na nossa barra temos apenas a força peso (aplicada no ponto médio), uma força vertical e uma horizontal (aplicadas no pino ) e o momento de binário.
Como nosso objetivo é apenas calcular o ângulo do equilíbrio, basta fazermos o somatório de momentos em relação ao ponto , o que elimina as reações do pino. Desta forma, temos:
No final, o difícil é resolver a equação acima... Bom, utilizando softwares para resolvê-la, chegamos ao valor:
E assim finalizamos a questão!