Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 37
As duas polias leves são presas uma à outra e formam uma unidade única. Elas são impedidas de girar em torno de seu mancal em por um cabo enrolado firmemente em torno da polia menor e preso ao ponto . Calcule o módulo da força suportada pelo mancal em para a carga aplicada de .
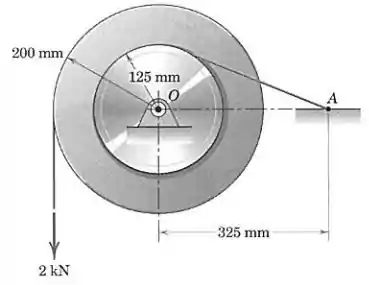
Passo 1
A força que atua ao longo do cabo dirigida para o ponto pode ser calculada por meio da equação de equilíbrio de momentos em torno de :
Passo 2
Através da equação de equilíbrio de forças na horizontal, podemos calcular a componente da força em :
onde é o ângulo que o cabo faz com a horizontal:
Então, podemos substituir os valores na equação:
Passo 3
Agora, usando a equação de equilíbrio de forças na vertical, calculamos a componente da força em :
Logo,
Resposta
Exercícios de Livros Relacionados
Determine as reações normais em A e B e a força na ligação CD agindo sobre o membro no problema 8
Determine as componentes horizontal e vertical da reação no pino C e a força na trva do guincho no problema 10
Se a mola BC esta descarregada com θ = 0 e a alavanca excêntrica atinge sua posição de equilíbrio quando θ = 15 , determine a força F aplicada perpendicularmente ao segmento AD e as componentes horizo
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pina A e a reação da s
O tubo de esgoto de 1,4 Mg é mantido nas pinças da empilhadeira. Determine as forças normais em A e B como funções do ângulo da lamina θ e represente graficamente os resultados de força(eixo vertical)