Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 22
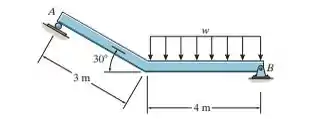
Se a intensidade da carga distribuída que atua sobre a viga é , determine as reações no rolete e no pino .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as reações no rolete (perpendicular ao plano inclinado) e no pino (forças paralelas e perpendiculares ao plano ).
Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Sempre que tiverem dúvida, voltem na Tabela 5.1 do livro! Lá são identificados os tipos de apoios com as suas reações!
Então, o nosso diagrama de forças será:
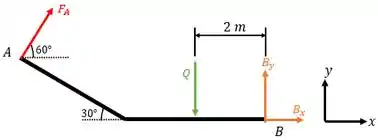
Um ponto importante que fizemos foi substituir o carregamento (carga constante ao longo do comprimento), por uma força aplicada no ponto médio do carregamento (a 2m do ponto ). Esta força é tal que:
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar calculando a reação no rolete . Para isto, temos que calcular o somatório do momento em relação ao ponto , pois assim eliminamos estas incógnitas da nossa equação.
Desta forma, temos:
E assim encontramos a nossa primeira reação!
Passo 3
Para finalizarmos a questão, temos que determinar as reações no pino . Para isto, vamos fazer o somatório das forças nas direções e .
Desta forma, temos:
Resolvendo as duas equações acima obtemos:
E assim finalizamos a questão!