O momento é aplicado a uma viga de seção transversal mostrada, em um plano formando um ângulo com a vertical. Determinar: (b) a tensão no ponto .
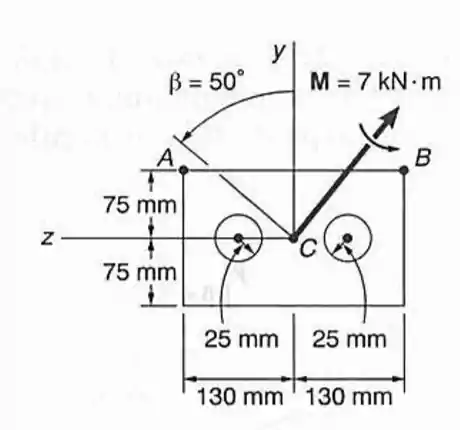
Passo 1
Problemas deste tipo serão resolvidos utilizando o seguinte passo-a-passo:
- Calcular os momentos de inércia do corpo em relação a cada eixo.
- Medir a distância do ponto que estamos analisando ao eixo.
- Decompor o momento em cada eixo.
- Aplicar a equação que relaciona tensão normal com momento fletor, que esta mostrada abaixo:
O problema pede o maior momento fletor permissível, que é dado pela equação:
Onde:
- é a tensão normal admissível.
- é o momento fletor.
- o momento de inércia.
- a maior distância entre o eixo e o ponto da peça.
Passo 2
Então vamos seguir nosso passo-a-passo e calcular o momento de inércia desse corpo para os dois eixos e . Começando pelo eixo :
Vamos lembrar que o momento de inércia da barra é:
Porém devemos substratir o efeito dos dois furos existentes na peça, para calcular o momento de inércia destes dois furos vamos fazer:
Logo o momento de inércia total é a diferença entre os dois valores:
Agora faremos a mesma coisa mas considerando o eixo :
Substraindo o efeito dos dois furos existentes na peça, para calcular o momento de inércia destes dois furos vamos fazer:
Logo o momento de inércia total é a diferença entre os dois valores:
Passo 3
Medir as distâncias:
Passo 4
Agora vamos decompor o momento nos eixos e :
Passo 5
Finalmente aplicar a equação do momento fletor:
Mas aqui temos de lembrar que existem dois momentos, um em cada eixo, então a nova tensão será calculada considerando os dois eixos:
Substituindo os valores: