Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 127
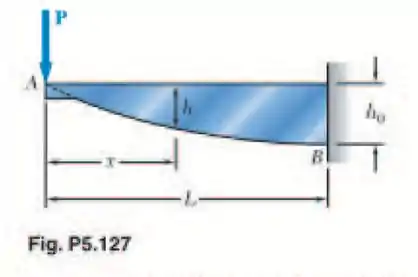
A viga AB, consistindo em uma placa de ferro fundido de espessura uniforme b e comprimento L, deve suportar a força mostrada. (a) Sabendo que a viga deve ser de resistência constante, expresse h em termos de x, L e . (b) Determine a força máxima admissível se L = 914 mm, = 305 mm, b = 31,8 mm e = 165 MPa.
Passo 1
Tá legal! Nesse exercício, não precisamos encontrar nenhuma reação de apoio para o sistema. Então podemos desenhar o diagrama de corpo livre para uma seção da viga com comprimento x, onde teremos:
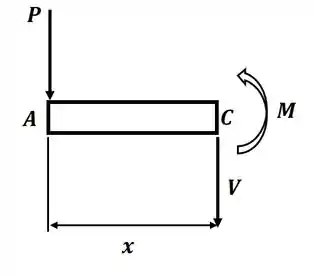
Agora, para esse DCL, vamos aplicar o somatório de momento em relação ao ponto C, para encontrar uma expressão para o momento M, então teremos:
Passo 2
Agora, vamos utilizar a equação 5.18 vista nessa seção para escrever o módulo de resistência da viga, que será dado por:
Substituindo a expressão para o momento encontrada no passo 1, teremos:
Agora, lembrando que o módulo de resistência para uma seção transversal retangular é dado por:
Podemos igualar as duas expressões encontradas para , fazendo isso, teremos:
Agora, isolando dessa equação, chegaremos em:
Passo 3
Ainda estamos na letra (a), vamos lá! Para escrever h em termos de x, L e , está faltando determinar o , que ocorre em , então, vamos substituir esse valor de na equação que encontramos para , chegando em:
Agora precisamos dar um jeito de fazer esse termo aparecer lá na equação de . Para isso, vamos dividir a equação de por dos dois lados, dessa forma, teremos:
Tá aí! Essa é a expressão que queríamos pra .
Passo 4
Agora para resolver a letra (b), vamos utilizar a equação que encontramos para :
E vamos isolar a força P, dessa forma, teremos:
Substituindo os valores conhecidos, temos: