Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 18

A montagem de barras lisas mostrada está em repouso quando é golpeada por um martelo em A com um impulso de 10 N.s. Determine a velocidade angular do conjunto e a intensidade da velocidade de seu centro de massa imediatamente após ele ter sido atingido. As barras têm uma massa por unidade de comprimento de 6 kg/m.

Passo 1

Para resolver esse exercício, iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício calculando a massa total do conjunto:

m = 3 6 0,4 → m = 7,2   k g

Agora, vamos encontrar o momento de inércia do conjunto em torno de seu centro de massa, lembrando que nesse caso separaremos o conjunto em três partes, a central, a inferior e a superior, e para as extremidades deveremos usar o teorema dos eixos paralelos:

I G = 1 12 6 0,4 0,4 2 + 2 1 12 6 0,4 0,4 2 + 6 0,4 0,2 2

I G = 0,288   k g . m 2

Passo 2

Agora podemos aplicar o princípio do impulso e da quantidade de movimento linear na direção y com o auxílio do esquema a seguir para descobrir o valor da velocidade nessa direção:

+ ↓       m v y 1 + ∑ ∫ t 1 t 2 F y d t = m v y 2

0 + 10 c o s 30 ° = 7,2 v y 2

v y 2 = 1,203   m / s

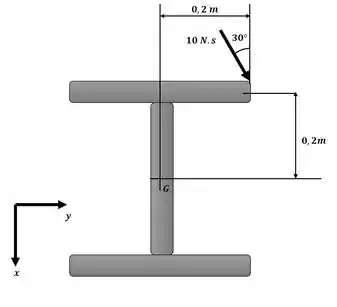
Agora podemos aplicar o princípio do impulso e da quantidade de movimento linear na direção x para descobrir o valor da velocidade nessa direção:

+ →     m v x 1 + ∑ ∫ t 1 t 2 F x d t = m v x 2

0 + 10 s e n 30 ° = 7,2 v x 2

v x 2 = 0,6944   m / s

Com as componentes da velocidade encontradas, podemos determinar o módulo da velocidade do centro de massa da seguinte forma:

v G = v G x 2 + v G y 2 = 0,6944 2 + 1,203 2

v G = 1,39   m / s

Passo 3

Agora podemos aplicar o princípio do impulso e momento angular para descobrir a velocidade angular final do conjunto:

↺ +   I G ω 1 + ∑ ∫ t 1 t 2 M G d t = I G ω 2

0 + - 10 c o s 30 ° 0,2 - 10 s e n 30 ° 0,2 = - 0,288 ω

ω = 9,5   r a d / s

Resposta

v G = 1,39   m / s

ω = 9,5   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois fios AC e BC estão amarrados a uma esfera de 7 kg que roda com uma velocidade escalar v no círculo horizontal mostrado na figura. Sabendo que θ 1 = 55° e θ 2 = 30° e que d = 1,4 m, determine o in
Trens pendulares como o American Flyer, que viaja entre Washington, Nova York e Boston, são projetados para viajar com segurança a altas velocidades em seções curvas de linhas férreas que foram constr
Um pequeno colar D de 300g pode deslizar sobre a parte AB de uma haste que é curvada, tal como mostra a figura. Sabendo que α = 40 ° e que a haste gira em torno da vertical AC a uma taxa constante de
Uma mesa rotativa A é construída em um palco para uso em uma produção teatral. Observa-se, durante um ensaio, que um baú B começa a deslizar sobre a mesa 10 s depois que ela começa a girar. Sabendo qu