Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 09
Se a corda é submetida a uma força horizontal P = 150 N, e a cremalheira está fixa ao plano horizontal, determine a velocidade angular da engrenagem em 4 s, partindo do repouso. A massa da engrenagem é 50 kg, e ela tem um raio de giração em relação a seu centro de massa O .
Passo 1
Começaremos esse exercício relacionando a velocidade linear do centro de massa com a velocidade angular da seguinte forma:
Passo 2
Antes de aplicarmos o princípio do impulso e da quantidade de movimento angular, devemos calcular o momento de inércia da engrenagem:
Passo 3
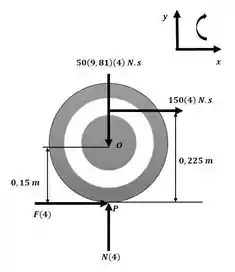
Agora podemos aplicar o princípio do impulso e da quantidade de movimento angular com o auxílio da figura a seguir:
Resposta
Exercícios de Livros Relacionados
A plataforma de 150 kg pode ser considerada como um disco circular. Dois homens, A e B, de 60 kg e 75 kg de massa, respectivamente, estão parados de pé na plataforma quando ela está em repouso. Se ele
Uma plataforma circular horizontal tem uma massa de 150 kg e um raio de giração k z = 2,4m em relação ao eizo z passando pelo seu centro O. A plataforma é livre para girar em torno do eixo z e está in
O corpo do satélite C tem uma massa de 200 kg e um raio de giração em relação ao eixo z de k z = 0,2m . Se o satélite gira em torno do eixo z com uma velocidade angular de 5 rev/s, quando os painéis s
Um homem de 75 kg salta para fora da plataorma circular com uma velocidade v m / p = 1,5m / s em relação à plataforma. Determine a velocidade angular da plataforma depois disso. Inicialmente o homem e
Duas crianças, A e B, cada uma tendo uma massa de 30 kg, estão sentadas na borda do carrossel que gira a ω = 2r a d / s . Excluindo as crianças, o carrossel tem uma massa de 180 kg e um raio de giraçã