Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 16

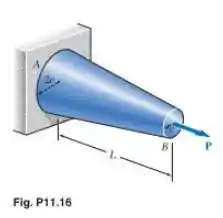
Mostre, por integração, que a energia de deformação da barra cônica A b   ´r:

U = 1 4 P 2 L E A m i n

Em que A m i n   é a área transversal em B .

Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiro, sabemos que a área da barra é:

A m i n = π c 2

Onde r = c x L .  

Logo:

A = π r 2 = π c 2 L 2 x 2

A integral é dada por:

U = ∫ L 2 L P 2 d x 2 E A = P 2 2 E ∫ L 2 L L 2 π c 2 d x x 2  

Resolvendo a integral:

U = P 2 L 2 2 W c 2 π - 1 x L 2 L

U = P 2 L 2 2 E A m i n - 1 2 L + 1 L

U = P 2 L 4 E A m i n

Prontinho, provado!

Resposta

U = P 2 L 4 E A m i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra A B é feita de um aço de alta resistência para o qual σ e = 750M P a e E = 200G P a . Uma energia de deformação de 25J deve ser acumulada pela barra quando a força axial P é aplicada. Sabendo-
Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
A barra A B é feita de um aço reforçado para o qual σ e = 275M P a e E = 200G P a . Uma energia de deformação de 5J deve ser acumulada pela barra quando a força axial P é aplicada. Sabendo-se que o di
Resolver o Prob. 10.23, suando a barra escalonada mostrada, como uma aproximação da barra em forma de tronco de cone. Qual é a porcentagem de erro na resposta obida?
Resolver o Prob. 10.25, assumindo que os dois diâmetros da barra, de 18m m e 19m m , foram aumentados para 21m m . Desta maneira, os três diâmetros à esquerda da barra de controle ficam constantes e d