Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 24
Resolver o Prob. 10.23, suando a barra escalonada mostrada, como uma aproximação da barra em forma de tronco de cone. Qual é a porcentagem de erro na resposta obida?
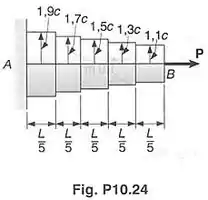
Passo 1
Fala, pessoal! Andam estudando muito? Ver questões passo a passo facilita, né? Então vamos resolver mais uma questão de energia de deformação! Animados?
Nessa questão, nós temos que comparar duas formas de calcular a energia de deformação de um tronco de cone. Em uma das formas, a gente considera que a área do tronco varia linearmente ao longo do cone. Foi assim que calculamos do cone no Prob. 10.23.
é a menor área da seção transversal do tronco de um cone. Se o raio dessa área for igual a , essa área vale .
A outra forma de se calcular a energia de deformação do cone é aproximando o cone como vários cilindros pequenos. A figura abaixo mostra a cone e a aproximação que fazemos dele.
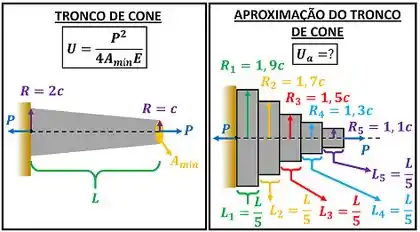
é a energia de deformação aproximada. é a energia de deformação do tronco de cone. Como a proximação do tronco é formada por cinco cilindros, a energia de deformação é a soma da energia desses cinco cilindros.
Para calcular a energia de deformação de cada um desses cilindros, usamos a equação 10.14 do livro. Essa equação é válida para barras com áreas da seção transversal constantes, como é o nosso caso!
Onde são as áreas dos cilindros , , , e , são os comprimentos dos cilindros , , , e e são as energias de deformação dos cilindros , , , e .
Para achar o erro percentual do cálculo de
Os tracinhos “|” que aparecem na fórmula do erro indicam que estamos usando o módulo.
No próximo passo vamos iniciar as contas, calculando as energias , , , e .
Passo 2
Nesse passo, vamos calcular . Para isso, é necessário calcular as áreas , , , e . Todas são calculadas a partir da fórmula . A única diferença entre essas cinco áreas são os valores diferentes de raio que cada uma tem.
Com esses valores podemos achar as energias de deformação , , , e de cada cilindro.
Passo 3
Nesse passo, vamos calcular a energia de deformação aproximada do tronco .
Somando as energias de deformação de cada cilindro, somos capazes de achar .
Colocando o termo em evidência, achamos:
Agora estamos prontos para calcular o erro relativo no próximo passo.
Passo 4
Esse é o último passo. Nele, vamos calcular o erro percentual da aproximação. Fazemos isso, substituindo os valores de e que conhecemos.
Cortando o termo , achamos: