Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 21
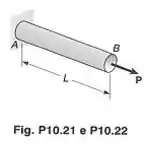
A barra é feita de um aço reforçado para o qual e . Uma energia de deformação de deve ser acumulada pela barra quando a força axial é aplicada. Sabendo-se que o diâmetro da barra é , determinar o comprimento da barra para a qual o coeficiente de segurança, em relação à deformação permanente, é seis.
Passo 1
Oieee! E aí, como você está? Vamos resolver um exercício de energia de deformação?
O enunciado quer que a gente calcule o comprimento da barra que faz o coeficiente de segurança ser igual a .
O coeficiente de segurança é a divisão entre a energia de deformação máxima que a barra atinge antes de se deformar permanentemente (quando a tensão é igual à tensão de escoamento ) e a energia de deformação que a barra tem ao ser tracionada com uma força .
Se a gente substituir por na fórmula acima, fica mais fácil de perceber o que o enunciado quer de verdade. Ele quer o valor do comprimento que faz ser vezes maior que .
A figura abaixo mostra todos os dados que precisamos para achar esse .
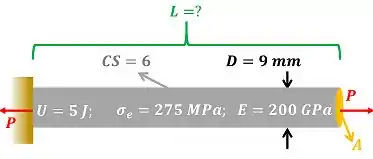
é a área da seção transversal da barra. é o diâmetro da barra. é o módulo de elasticidade da barra. é a máxima tensão que a barra pode sofrer sem se deformar permanentemente.
Para achar a energia de deformação máxima , precisamos achar a máxima carga que causa essa deformação máxima. Essa carga é igual à tensão vezes .
Para calcular a energia de deformação a partir da força precisamos usar a equação 10.14 do livro. Esse equação é válida para barras com áreas da seção transversal constantes, como é o nosso caso!
Agora que temos todas essas informações em mãos, vamos calcular o comprimento da barra nos próximos passos!
Passo 2
Agora, vamos cumprir a primeira etapa que precisamos para achar o comprimento . Nessa etapa, vamos calcular a área , depois calcularemos e, por último, calcularemos .
Então vamos iniciar, achando a área em .
Oba, fizemos a primeira parte! Agora vamos partir para o cálculo de ! Antes, para a força dar um resultado em newton , temos que lembrar que a tensão de escoamento é igual à .
Agora estamos prontos para encerrar a primeira etapa, calculando a energia de deformação !
Agora que temos todos esses valores, podemos substituir todos os termos da outra equação de para achar o valor do comprimento !
Passo 3
Nesse passo, vamos enfim achar o valor de . Mas não se apresse. Para o resultado da conta dar em metro , precisamos converter o módulo de elasticidade de para .
Fazemos isso, multiplicando o valor de em por .
Substituindo esse valor na equação de , ela vira:
Isolando o em um lado da equação e passado todos os outros termos para o lado oposto, achamos:
Uhuuuul! Achamos o comprimento ! Bate aqui!
