Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 8

O diagrama tensão-deformação mostrado foi construído com base em dados obtidos durante um teste de tração de uma barra de uma liga de alumínio com diâmetro de 5 8 i n .   Sabendo que a deformação foi medida usando-se um comprimento de referência de 180   i n   determine (a) o módulo de resiliência da liga e (b) o módulo de tenacidade.

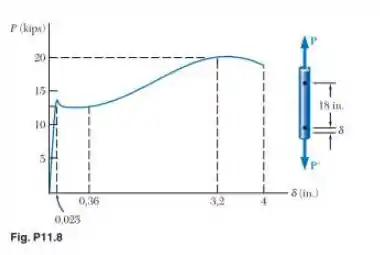
Passo 1

Fala aí, galera. Tudo bem? Bora pra outra questão.

Primeiramente, com o diâmetro, podemos obter a área da seção, que será:

A = π 4   5 8 2 = 0,6068   i n 2

Com a área e a força de escoamento, tirada do gráfico, temos a tensão de escoamento:

σ = P A = 12,5   k i p s 0,3068   i n 2 = 40   k s i

Agora, através do gráfico e do comprimento dado, pode-se determinar a deformação de escoamento:

ε δ L = 0,025   i n 18   i n = 1389   × 10 - 3  

Passo 2

Agora, vamos determinar o módulo de resiliência. Ele será:

u y = 1 2   σ y ε y

Onde a tensão e deformação são as de escoamento. Logo:

u y = 1 2 40 × 10 3 1389 × 10 - 3 = 28   l b i n 2

Passo 3

Agora, o módulo de tenacidade será a área do diagrama de tensão e deformação da parte elástica (linear). Logo:

A = 28 + 40 0,02 - 0,0014 + 1 2 40 + 65 0,1778 - 0,02 + 62,5 0,222 - 0,1778

A = 13,4   l b / i n

Resposta

  1. u y = 28   l b i n 2
  2. A = 13,4   l b / i n
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em muitas aplicações de carregamento, sabe-se que a tensão normal numa dada direção é nula, como por exemplo, σ z = 0 , para o caso da placa fina mostrada. Para este caso, conhecido como o estado plan
Em muitas situações físicas, os vínculos impedem que as deformações especificas ocorram em uma dada direção, por exemplo, ε z = 0 , para o caso mostrado, onde o movimento longitudinal de qualquer pont
Para a barra composta do P r o b .2.10 6 , determinar a tensão residual em cada lâmina, se P cresce gradualmente desde zero até 357k N e então, decresce até zero.
Para a barra composta do P r o b .2.104 , determinar a tensão residual em cada porção da barra, se P cresce gradualmente desde zero até a deflexão do ponto C atingir um valor máximo δ m e então decres
Uma barra de aço de comprimento L e seção transversal uniforme de área A , está fixada na extremidade a dois suportes rígidos e ausente de tensões a uma temperatura de 20 ° C . o aço é assumido ser el