Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 56
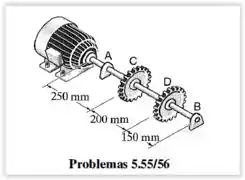
O motor transmite ao eixo de aço inoxidável 304 quando gira a . O eixo tem diâmetro de e está apoiado em mancais lisos em e , que permitem a livre rotação do eixo. As engrenagens e presas ao eixo absorvem e , respectivamente. Determine a tensão máxima absoluta no eixo e o ângulo de torção da engrenagem em relação à engrenagem .
Passo 1
Olá, pessoal! Tudo bem com vocês?
O enunciado nos fornece os seguintes dados:
Aço inoxidável 304, portanto,
Só que sabemos que a potência fornecida pelo moto deve ser divida pelas duas engrenagens, portanto se a engrenagem recebe , então a engrenagem vai receber e não .
Não é fornecida a rotação do eixo, mas podemos encontrá-la usando a frequência:
Passo 2
Vamos observar o diagrama de corpo livre:
Calculando os torques:
age na seção , então .
Na engrenagem :
Na seção , fazendo o somatório dos momentos, temos que:
E na engrenagem :
E, portanto, .
Passo 3
Primeiro vamos encontrar a tensão de cisalhamento máxima, através da equação:
Em que é o raio e o momento polar de inércia, , é dado por:
Que substituindo em , fica:
Aplicando os valores, temos:
Passo 4
Vamos agora calcular o ângulo de torção!
Que substituindo o , fica:
Agora colocando todos os dados, temos:
Convertendo para graus: