Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 48

Resolver o Prob. 3.47, considerando que AB é feito de aço ( G = 77   G P a ) , ao invés de alumínio

Passo 1

A melhor forma de começar as questões de torção é calculando os momentos de inércia.

Passo 2

Vamos fazer uma seção no ponto B:

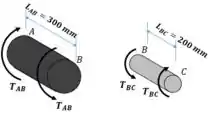
Como é uma situação estática, podemos afirmar que:

T = T A B + T B C

12,5 = T A B + T B C

Beleza! Mas e agora? A equação acima não é suficiente para determinar T A B e T B C . Precisamos de uma outra forma de relacionar esses torques!

Se a gente observar melhor, vamos ver que no ponto B as duas barras estão engastadas. Isso quer dizer que as duas barras devem ter o mesmo ângulo de torção ϕ ! Vamos usar isso para determinar os torques.

Primeiro calculamos o ângulo de torção em cada barra:

T o r ç ã o   n a   b a r r a   A B T o r ç ã o   n a   b a r r a   B C ϕ A B = T A B L A B J A B G A B ϕ B C = T B C L B C J B C G B C

E igualamos:

ϕ A B = ϕ B C

T A B L A B J A B G A B = T B C L B C J B C G B C

Vamos isolar T A B :

T A B = T B C ⋅ L B C J B C G B C ⋅ J A B G A B L A B

T A B = T B C ⋅ 200   m m 988769,5 π ⋅ 39   G P a ⋅ 7629394,5 π ⋅ 77   G P a 300   m m

Calculando, a gente tem a relação:

T A B = 10,16   T B C

Passo 3

Agora está super fácil! Basta resolver o sistema abaixo:

12,5 = T A B + T B C T A B = 10,16   T B C

Logo:

T B C = 1,12   k N m

T A B = 11,38   k N m

Passo 4

Agora vai ser super fácil calcular as tensões.

Primeiro vamos calcular o raio de A B

c A B = D 2 = 125   m m 2 = 62,5   m m

A questão já ta no papo! Agora é só aplicar a fórmula da tensão de cisalhamento

τ A B = T A B c A B J A b = 11,38   k N m ⋅ 62,5   m m 7629394,5 π   m m 4

τ A B = 2 9,7   M P a

Passo 5

Vamos repertir a mesma coisa para calcular a tensão em BC

Calculamos o raio:

c B C = d 2 = 75   m m 2 = 37,5   m m

A questão já ta no papo! Agora é só aplicar a fórmula da tensão de cisalhamento

τ B C = T B C c B C J B C = 1,12   k N m ⋅ 37   m m 988769,5 π   m m 4

τ B C = 13,52   M P a

Resposta

T B C = 1,12   k N m

T A B = 11,38   k N m

τ A B = 29,7   M P a

τ B C = 13,52   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo sólido mostrado é feito de aço doce considerado elastoplástico com T E = 145M P a . Determine o raio do núcleo elástico causado pela aplicação de um torque igual a 1,1T E em que T E é a intensi
Observa-se que um clipe de papel pode ser girado por várias voltas com a aplicação de um torque de proximidade 60 m N ⋅ m . Sabendo que o diâmetro do fio utilizado no clipe é de 0,9 m m , determine o
O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura ( G l a t ã o = 39G P a ) ã unido a um núcleo de aço de 40 mm de diâmetro G a ç o = 77.2G P a ç . Sabendo que o eixo e
O eixo sólido mostrado é feito de um aço baixo carbono considerando elastoplástico com G = 77,2G P a e t E = 145M P a . determine o ângulo de giro produzido pela aplicação de um torque de intensidade
O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura ( G l a t ã o = 39G P a ) ã unido a um núcleo de aço de 40 mm de diâmetro G a ç o = 77.2G P a ç . As tensões de cisalh