Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 47b
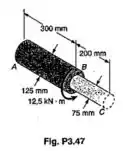
Os cilindros maciços AB e BC estão unidos em B e engastados em A e C. Sabendo-se que AB é de alumínio e BC é de latão , determinar para o carregamento mostrado: (a) a reação em cada extremidade fixa; (b) a máxima tensão de cisalhamento em AB; (c) a máxima tensão de cisalhamento em BC
Passo 1
Primeiro vamos calcular o raio de
A questão já ta no papo! Agora é só aplicar a fórmula da tensão de cisalhamento
Resposta
Exercícios de Livros Relacionados
Determine o ângulo pelo qual a extremidade A gira quando T = 565N ⋅ mm, l = 61 mm, d = 1,59 mm, G=77,2 GPa e n=2 .
Dois eixos, cada um com diâmetros de22 , 2m m , são conectados pelas engrenagens mostradas na figura. Sabendo que G=77 , 2G P a e que o eixo está fixo em F , determine o ângulo pelo qual a extremidade
Três pontos do diagrama tensão-deformação usado no Prob. 3,112 são 0 ; 0 ,0,0015 ; 55M P a ,e0,003 ; 80M P a . Ajustando a polinomial T = A + B γ + C γ ² ²por esses pontos, a seguinte relação foi obti
O eixo de aço doce mostrado na figura é considerado elastoplástico com G = 77,2G P a e t E = 145M P a .Determine a máxima tensão de cisalhamento e o raio do núcleo elástico causado pela aplicação de u
O eixo circular de seção cheia mostrado na figura é feito de um aço considerado elastoplástico com t E = 145M P a . Determine a intensidade do torque T aplicado quando a zona plástica tem (a) 16 m m d