Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 13
Considerando que a massa de um barril cheio somado com seu conteúdo tem uma massa combinada de . Um cilindro C é ligado ao barril na altura como mostra figura. Sabendo que , determine o peso Maximo de C para o qual o barril não tombará.
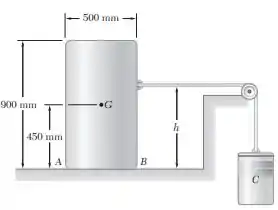
Passo 1
Cinemática: suponha que o barril está deslizando, mas não inclinando.
Uma vez que o cabo é inextensível,
Cinética: desenhe os diagramas de corpo livre do cano e do cilindro.
O barril esta deslizando
Suponha que o tombamento seja iminente, de modo que a linha de ação da reação no fundo do barril passe pelo ponto B.
Passo 2
Para o barril
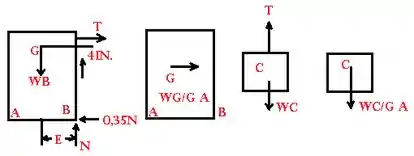
Para o cilindro:
Resposta
Exercícios de Livros Relacionados
Uma viga de 15 pés pesando 500 lb é abaixada por meio de dois cabos desenrolados de pontes rolantes. Conforme a viga se aproxima do solo, os operadores do guindaste acionam os freios para diminuir o m
Uma viga de 15 pés pesando 500 lb é abaixada por meio de dois cabos desenrolados de pontes rolantes. Conforme a viga se aproxima do solo, os operadores do guindaste acionam os freios para diminuir o m
O rolo de aço mostrado tem uma massa de 1.200 kg e um raio de rotação centróide de 150 mm, e está sendo baixado por dois cabos enlaçados em torno de seu eixo. Sabendo que no instante mostrado a aceler
O ioiô de 3 onças mostrado tem um raio de giro centroide de 1,25 pol. O raio do tambor interno no qual uma corda é enrolada é de 0,25 pol. Sabendo que no instante mostrado a aceleração do centro do io
Para o caminhão do Problema resolvido 16.1, determine a distância que ele vai derrapar se (a) os freios traseiros não funcionarem, (b) os freio dianteiros não funcionarem.