Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 21
Uma mulher faz exercícios na máquina de remada. Se ela exerce uma força de na alavanca , determine as componentes horizontal e vertical de reação no pino e a força desenvolvida sobre a alavanca ao longo do cilindro hidráulico
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as reações no pino de apoio e no cilindro hidráulico (uma correção aqui galera! Houve erro de digitação ao dizer que o cilindro era BC).
Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Sempre que tiverem dúvida, voltem na Tabela 5.1 do livro! Lá são identificados os tipos de apoios com as suas reações!
Considerando todo o equipamento como corpo rígido, teremos apenas a ação da força e das reações nos pinos e . Então, o nosso diagrama de forças será:
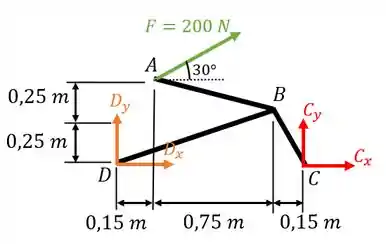
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar calculando a reação vertical . Um ponto que nos ajudará bastante é perceber que os pontos e pertencem ao mesmo segmento horizontal!
Então, começando pelo somatório de momentos em torno do ponto , temos:
Não precisamos calcular , pois a questão não pediu, e também porque teremos uma sacada agora que vai facilitar o resto da questão!
Passo 3
Vamos fazer um recorte agora na estrutura para que apareça a força do cilindro hidráulico. Com isto, teremos uma força na mesma direção do cilindro, como podemos ver no seguinte esboço.
Agora vai ficar fácil calcularmos as outras reações! Por exemplo, para calcularmos a reação , basta fazermos:
E chegamos a nossa reação!
Passo 4
Por fim, nos resta determinarmos a força . Vamos determinar as componentes ortogonais e inicialmente.
Então, fazendo o somatório de forças para o desenho do Passo 3, temos:
Resolvendo o sistema acima, obtemos:
E assim, teremos que a intensidade da força será:
E assim finalizamos a questão!