Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 50

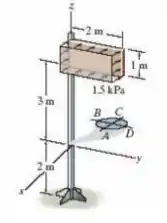
O painel de sinalização está sujeito à carga uniforme do vento. Determine as componentes da tensão nos pontos C e D no poste de sustentação de 100 mm de diâmetro. Mostre os resultados em um elemento de volume localizado em cada um desses pontos

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que esse painel recebe uma carga uniforme na sua superfície, e nos pede o estado de tensão nos pontos C e D da seção transversal. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu??

Passo 2

Nosso primeiro passo será calcular nossas forças internas, ou seja, a normal, os momentos e os cortantes.

→ ∑ F x = 0

  V x = 3   k N      

↑ ∑ F y = 0

V y = 0   k N  

→ ∑ F z = 0

N z = 0   N      

↶ ∑ M y = 0

M y = 3   x   3,5 = 10,5   k N . m

↶ ∑ M z = 0

T z = 3   k N . m

Passo 3

Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.

σ c =     N z A -   M y   x c I = 0 - 10,5   x   0,05   x   10 3 0,25 π   0,05 4 = - 107   M P a

τ c =   V Q c I t + τ x c o J =   3   x   10 ³   x   0,05 0,5 π   0,05 4   = 15,3     M P a

σ d =     N A +   M y   z d I = 0   M P a

τ d =   V Q d I t + τ x c o J =   3000 2 0,05 3 3 0,25 π   0,05 4 0,01 + 3   x   10 3 x   0,05 0,5 π   0,05 4   = 1 5 , 8     M P a

Resposta

σ c =   -   107   M P a

τ c = 15,3     M P a

σ d = 0   M P a

τ d =   1 5 , 8     M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto A e mostre os resultados em um elemento de volume diferencial nesse ponto.
A barra tem diâmetro de 40 mm. Se sua extremidade for submetida às duas componentes de força mostradas na figura, determine o estado de tensão no ponto B e mostre os resultados em um elemento de volum
A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto B e mostre os resultados em um elemento de volume diferencial nesse ponto.
O guindaste AB consiste em tubo que é usado para levantar o feixe de hastes que tem massa total de 3 Mg e centro de massa em G. Se o tubo tiver diâmetro externo de 70 mm e 10 mm de espessura de parede
O eixo de 18 mm de diâmetro é submetido à carga mostrada na figura. Determine as componentes da tensão no ponto B. Trace um rascunho dos resultados em um elemento de volume localizado nesse ponto. O m