Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 48

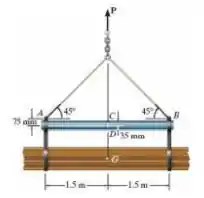
O guindaste AB consiste em tubo que é usado para levantar o feixe de hastes que tem massa total de 3 Mg e centro de massa em G. Se o tubo tiver diâmetro externo de 70 mm e 10 mm de espessura de parede, determine o estado de tensão que age no ponto D. Mostre os resultados em um elemento de volume diferencial localizado nesse ponto. Despreze o peso do tubo.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa barra recebe duas forças na sua ponta, e nos pede o estado de tensão no ponto D da seção transversal. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu??

Passo 2

Nosso primeiro passo será calcular nossas forças internas, ou seja, a normal, o momento e o cortante, uma vez que sabemos que seu peso é dado por:

W = 3   x   10 ³   x   9,81 = 29,43   k N

↑ ∑ F y = 0

T   s e n 45 ° = 0,5   x   29,43       ∴       T = 20,81

→ ∑ F x = 0

  N x = 20,81 cos ⁡ 45 ° = 14,715   k N      

  ↶ ∑ M = 0

M = 20,81   s e n 45 ° x   1,5 - 14,715   x   1,5 + 20,81 cos ⁡ 45 ° x   0,075 = 1,10362     k N . m

Passo 3

Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.

σ d =   -   N A +   M y   z d I = - 14,715   x   10 3 π   0,035 2 - 0,025 2 + 1,10362   x   10 3 x   0 0,25 π   0,035 4 - 0,025 4 = - 7,81   M P a

τ d =   V Q d I t = 0     M P a

Resposta

σ d = - 7,81   M P a

τ d = 0   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga de abas largas está sujeita à carga mostrada na figura. Determine as componentes da tensão nos pontos A e B e mostre os resultados em um elemento de volume em cada um desses pontos. Use a fórmu
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto A. O suporte tem 12 mm de espessura.
O bloco está sujeito às duas cargas axiais mostradas na figura. Faça um rascunho da distribuição da tensão normal que age na seção transversal no corte a-a. Despreze o peso do bloco.
O pino de suporte sustenta a carga de 3,5 kN. Determine as componentes da tensão no elemento estrutural do suporte no ponto B. O suporte tem 12 mm de espessura.
A viga suporta a carga mostrada na figura. Determine o estado de tensão nos pontos E e F na seção a-a e represente os resultados em um elemento de volume diferencial localizado em cada um desses ponto