Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 57
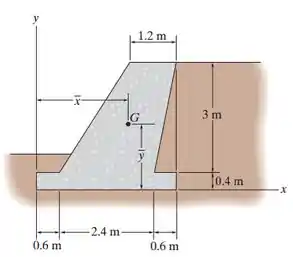
A parede de gravidade é feita de concreto. Determine a localização do centro de massa para a parede.
Passo 1
Faaala! Queremos a coordenada e a do centroide dessa parede. Como ela tem esse formato estranho, vamos precisar dividir nosso muro em partes mais simples e usar as fórmulinhas:
Repara:
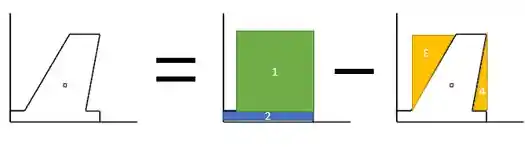
Nós conseguimos formar nossa figura se a gente pegar esse conjunto azul/verde e tirar os triângulos.
Então o que a gente pode fazer é calcular os dessas figuras coloridas. E aí para chegar no centroide da nossa figura, as áreas dos triângulos amarelos entram negativas quando formos usar as fórmulinhas.
Vamos fazer isso!
Passo 2
A gente precisa da área e das coordenadas do centroide de cada figura separadamente.
Utilizando uma tabela de centroides encontramos as fórmulas dessas grandezas para cada formato desses e identificamos seus centroides. Para o retângulo, o centroide é no meio. E para o triângulo, o centroide fica a da base.
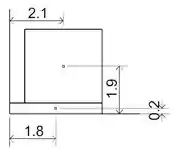
Como retângulo maior tem 2,4 m de largura, a gente divide isso por dois e soma a distância desse retângulo até o eixo coordenado . Aí ficamos com
Fazemos algo parecido para , a gente divide a altura por e soma a distância de :
Aí a gente repete esse raciocínio para o retângulo menor. Marcamos as coordenadas dos centroides deles na figura.
Passo 3
Olhando para os triângulos:
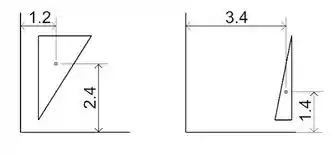
Vamos olhar para o triângulo da esquerda. O centroide fica a da base. Mas como a ponta dele está mais perto do eixo , nós podemos calcular fazendo da altura e somar com a distância do triângulo até o eixo :
Já em relação a , a situação muda, porque a base vertical está mais perto de , então o que a gente pode fazer é calcular um terço da base paralela a , e somar com a distância ao eixo . Fica
Para o outro triângulo também temos que ter essa atenção em como ele está posicionado em relação aos eixos, e fazer raciocínios parecidos. Aí nossas coordenadas são essas da figura.
Passo 4
Vamos agora montar uma tabela com nossos dados, para os triângulos a área é negativa pois precisamos subtraí-los. Aqui a gente já aproveita e calcula nossos valores de somatório para jogar na fórmulinha.
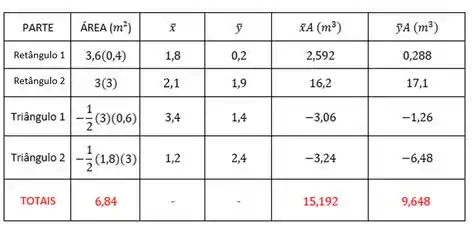
Ficando com:
Logo,