Uma partícula de 2 kg desloca-se ao longo de uma trajetória definida por r = 3 + 2 t 2m , θ = 1 3 t 3 + 2r a d E z = ( 5 - 2 t 2 ) m, onde t é dado em segundos. Determine as componentes da força r , θ , z que a trajetória exerce sobre a partícula no instante t = 1 s.

F r = - 32N F θ = 36N F z = - 8N

Enunciado

O enunciado nos dá as seguintes informações:

Massa da partícula: kg

Coordenadas polares.

Sabemos que a trajetória do movimento é descrita por:

Desenhando o diagrama de corpo livre, temos

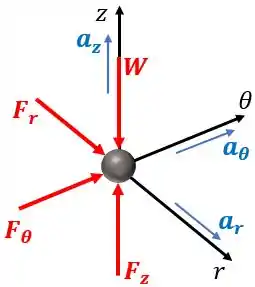
Onde é a força peso e .

A partir desses dados, devemos determinar as componentes da força , e sobre a partícula quando s.

Primeiramente, vamos encontrar as derivadas temporais de ( e ):

As derivadas temporais de ( e ):

Substituindo s nas equações encontradas, temos que

Sabemos que as componentes da aceleração nas coordenadas , e são dadas por

Logo, em

Os valores de e negativos nos dizem que estas acelerações atuam no sentido oposto ao desenhado no diagrama de corpo livre.

Agora aplicaremos as Equações do Movimento para resolver o problema.

Analisando primeiramente no eixo , temos que

Analisando no eixo , temos

Os valores de e negativos nos dizem que estas componentes da força atuam no sentido oposto ao desenhado no diagrama de corpo livre.