Exercícios de Coordenadas Polares, Tangenciais e Normais - Lista de Exercícios Resolvida

Um motorista que dirige ao longo de um trecho de reta de uma rodovia diminui a velocidade de seu automóvel para uma taxa constante antes de sair da rodovia em direção a uma rampa de saída circular com raio de . Ele continua a desaceleração com a mesma taxa constante de tal forma que, após ter entrado na rampa, sua velocidade escalar diminuiu para , uma velocidade escalar que ele, então, mantém. Sabendo que a essa velocidade constante a aceleração total do carro é igual a um quarto de seu valor antes de entrar na rampa, determine o valor máximo da aceleração total do carro.

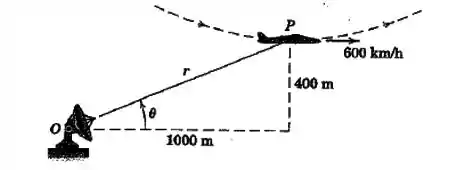
Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo em um plano vertical () a uma altitude de metros, o avião tem uma velocidade horizontal de e nenhuma aceleração horizontal. O raio de curvatura da trajetória é . Para o radar de rastreamento em , determine os valores de e registrado para esse instante.

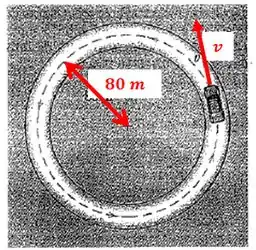
Um carro de teste parte do repouso em uma pista horizontal circular de de raio e aumenta sua velocidade a uma taxa uniforma para atingir os em segundos. Determine o módulo da aceleração total do carro segundos após a partida.

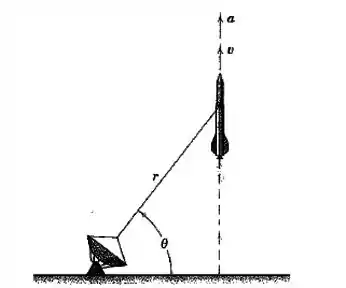
O foguete é lançado verticalmente e rastreado pela estação de radar mostrada. Quando chega a , outras medições correspondentes fornecem os valores , , . Calcule o módulo da velocidade e da aceleração do foguete nesta posição.

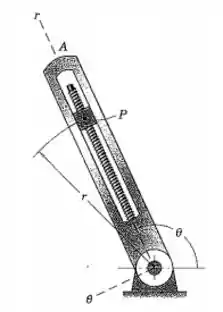
O movimento do bloco deslizando na ranhura radial rotativa é controlado pelo parafuso como mostrado. Para o instante representado , e . Além disso, o parafuso gira a uma velocidade constante fornecendo . Para este instante, determine os módulos da velocidade e da aceleração de . Desenhe e a para .

Na parte inferior da acrobacia aérea na qual o avião descreve um círculo em um plano vertical, o módulo da aceleração total do avião é de . Se a velocidade do avião em relação ao ar é de e está aumentando na taxa de por segundo, calcule o raio de curvatura da trajetória em .

03) Sabendo que um ponto se move de acordo com a equação

Pede-se determinar, para o instante t=1s:

a) a expressão intrínseca da velocidade de

b) os versores do triedro de Frenet (tangente, normal e binormal)