Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 115
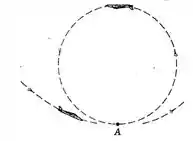
2/115) Na parte inferior A da acrobacia aérea na qual o avião descreve um círculo em um plano vertical , o módulo da aceleração total do avião é de . Se a velocidade do avião em relação ao ar é de e está aumentando nataxa de por segundo , calcule o raio de curvatura da trajetória em A .
Passo 1
Então galera , a aceleração tangencial pode ser facilmente obtida pela fórmula :
Para acharmos aaceleração normal , podemos usar a relação :
Passo 2
Agora , que temos a aceleração norma , podemos achar o raio de curvatura da trajetória, uma vez que :
Resposta
De boa pessoal? Bora continuar então
Exercícios de Livros Relacionados
2/135) Um carro P se desloca ao longo de uma estrada reta com uma velocidade constante v = 100 k m / h . No instante em que o ângulo θ = 60 ° , determine os valores de r ' em m / s e θ ' em graus/s .
2/145) Um mecanismo interno é usado para manter uma velocidade angular constante Ω = 0,05r a d / s em torno do eixo z da espaçonave enquanto as hastes telecópicas são prolongadas a uma taxa constante
2/142) Enquanto o cilindro hidráulico gira em torno de O , o comprimento exposto l da haste do pistão P é controlado pela ação da pressão do óleo no cilindro . Se o cilindro gira na taxaconstante θ '
2/137) O movimento do bloco deslizante P na ranhura radial rotativa é controlado pelo parafuso como mostrado . Para o instante representado θ ' = 0,1 r a d / s , θ " = - 0,4 r a d / s 2 e r = 300 m m
2/139) A haste O A B gira em torno do ponto O , enquanto a seção A B simultameamente prolonga-se de dentro da seção O A . Determine a velocidade e a aceleração do centro B da polia para as seguintes c