Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 108

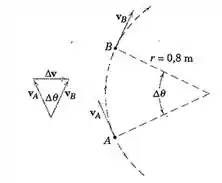
2/108 ) Uma partícula se desloca sobre uma trajetória circular de raio r = 0,8   m com uma velocidade constante de 2   m / s . A velocidade sofre uma variação vetorial ∆ v de Apara B . Expresse o módulo de ∆ v em termos de v e ∆ θ e divida-o pelo intervalo de tempo ∆ t entre A   e B para obter o módulo daaceleração média da partícula para (a) ∆ θ = 30 ° , (b)   ∆ θ = 15 ° e (c) ∆ θ = 5 ° . Em cada caso , determine a diferença percentual para o valor instantâneo da aceleração .

Passo 1

Então galera , nós sabemos que :

v a = v b = v = 2 m s

Além disso , temos que :

∆ v = 2 v sen ⁡ ∆ θ 2 = 4 sen ⁡ ∆ θ 2 m / s

∆ t = r ∆ θ v = 0.8 ∆ θ 2 = 0.4 ∆ θ

a a v = ∆ v ∆ t = 4 sen ⁡ ∆ θ 2 0.4 ∆ θ = 5   sen ⁡ ∆ θ 2 ∆ θ 2

A aceleração pode ser obtida por :

a n = v 2 r = 2 2 0.8 = 5 m / s 2

Para o primeiro caso :

∆ θ = 30 °             ∆ θ 2 = 15 °             ∆ θ 2 r a d = 0.262             sen ⁡ ∆ θ 2 = 0.259             a a v 1 = 4.94 m s 2  

Diferença percentual : 1,1   %    

Passo 2

Para o segundo caso : ∆ θ = 15 °             ∆ θ 2 = 7,5 °             ∆ θ 2 r a d = 0.1309             sen ⁡ ∆ θ 2 = 0.1305             a a v 1 = 4.99 m s 2  

Diferença percentual : 0.3   %

Passo 3

Para o terceiro caso :

∆ θ = 5 °             ∆ θ 2 = 2,5 °             ∆ θ 2 r a d = 0.0436             sen ⁡ ∆ θ 2 = 0.0436             a a v 1 = 4.998 m s 2  

Diferença percentual : 0.03 %

Resposta

Diferença percentual de 1,1 % , 0,3 % e 0,03 % respectivamente .

De boa pessoal? Bora continuar então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2/156) O carro A está se deslocando com velocidade constante v sobre a rodovia reta e horizontal . O oficial de polícia no carro estacionado P tenta medir a velocidade v com radar . Se o radar mede a
2/146) A posição radial de umapartícula P de fluido em umadeterminada centrífuda com palhetas radiais é aproximada por r = r 0 cos ⁡ h K t , onde t é tempo e k = θ ' é a velocidade angular constante n
2/167) Um meteoro P é rastreado por um radar observatório sobre a terra em O . Quando o meteoro está diretamente acima ( θ = 90 ° ) , as seguintes observações são registradas : r = 80k m , r ' =- 20 k
2/159) No instante representado na figura , a estação de radar em O mede a taxa de variação do ônibus espacial P como sendo r ' = - 3742 m / s , com O considerado fixo . Sabendo-se que o ônibus espapc
2/153) Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo em um plano vertical ( r - θ ) a uma altitude de 400 metros , o avião P tem uma velocidade horizontal de 600 k m / h