Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 69
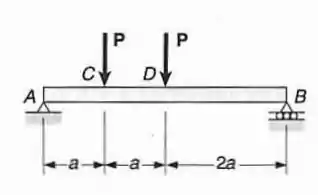
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares,escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar o máximo momento fletor da viga.
Passo 1
Agora a gente vai resolver os problemas com a utilização de funções singulares, mas o que é isso? Olha a função abaixo:
Esse é uma função normal, correto? Mas imagina que eu quero fazer o seguinte: Ignorar o segundo termo quando . Nós podemos fazer escrevendo:
Dessa forma vamos admitir duas hipóteses:
Quando a função fica:
Quando a função fica:
Legal né? É essa propriedade que vamos utilizar neste problema.
Passo 2
Vamos calcular as reações nos pontos e . Para isso vamos fazer o somatório das forças em igual a zero (é um problema de estática, lembre-se):
Como existe apenas uma força em essa força é nula, logo . Podemos partir para o somatório do momento:
Considerando o eixo positivo horário vamos ter:
Logo,
Passo 3
Pessoal aqui vamos colocar direto a equação da força cortante e você vai ver como é simples quando existem apenas forças pontuais:
Vou explicar cada termo com calma. Entre os pontos e existirá apenas um termo isso porque a cortante será igual à própria força de reação em .
Quando então vamos ter que a força cortante será igual a:
O termo representa que a força irá aparecer influenciando a cortante apenas quando .
Por fim quando vamos ter:
Como a gente sabe o valor de podemos substituir e achar, na forma geral:
Passo 4
Para achar o momento basta que a gente integre :
Tranquilo né? A gente só tem que saber quem é a constante . Essa constante tem o valor igual ao do momento puro aplicado na barra, mas como não existe momento puro nesse caso então:
Logo,
Passo 5
Para achar o ponto onde o momento é máximo a gente precisa zerar a força cortante e achar o ponto onde isso acontece
Pessoal, vamos ter que criar 3 hipóteses. Uma quando outra quando e outra quando .
Claramente não é possível termos , correto?
Aqui também não é possível!
Ixiii e agora? Deu ruim? Não existem nenhum ponto com ?
Claro que existe, perceba que entre 2 e 3 o sinal de mudou? Então necessariamente ocorreu um ponto onde a força cortante era zero, e esse ponto ocorre exatamente em , pois logo antes desse ponto era positivo e logo após passou a ser negativo.
Passo 6
Com isso vamos substituir na equação do momento fletor:
Como então todos os termos entram na conta!
Resposta
a)
b)