Usando o método da Sec 7.4, resolver o prob. 7.25
Passo 1
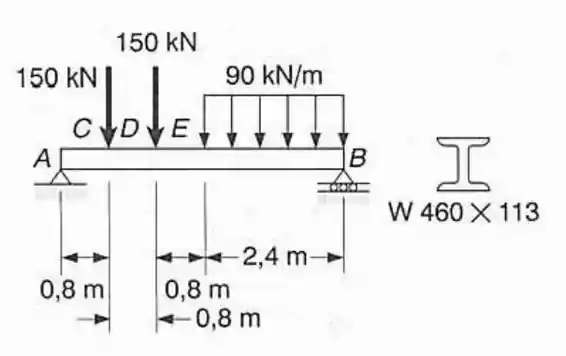
Fala aí, galera! Para resolver esse problema vamos utilizar o método da seção 7.4 que nos traz uma maneira mais prática de achar os momentos fletores e forças cortantes.
Esse método é baseado no fato da força cortante ser igual a derivada do momento fletor. Com isso vamos poder achar o momento fletor integrando a força cortante da seguinte forma:
Além disso vamos calcular a força cortante bem rapidamente também analisando apenas as forças líquidas na seção.
Vamos ver com mais calma conforme vamos resolvendo, então partiu!
Passo 2
A primeira coisa que devemos fazer é um diagrama das forças de modo a achar as forças de reação:
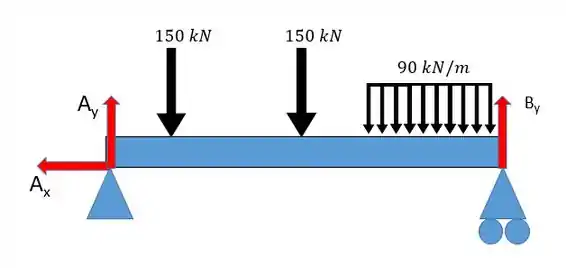
Como só existe uma força na horizontal podemos já dizer logo que ela é nula, logo . Agora vamos partir para as forças verticais:
Observando que o termo representa o valor da força distribuída que vale:
Assim,
Fazendo o somatório dos momentos em relação ao ponto e assumindo o sentido horário positivo:
Lembrando que a força distribuída atua na metade do carregamento.
Continuando
Logo,
Passo 3
Pronto! Agora vamos achar a força cortante, como já havia dito a força cortante será igual ao valor líquido das forças anteriores a ela.
Então para a seção vamos ter:
Agora para achar o momento fletor basta integrar esse valor:
Aqui a gente vai achar o momento fletor no ponto , isso porque o momento fletor nas pontas sempre será igual a zero, beleza? Então
Utilizamos e porque são os pontos que representam e
Como o problema pede a máxima tensão normal numa seção transversal a vamos ter que calcular também:
Para isso vamos ter que ter a força cortante:
Subsituindo:
Lembrando que cada nova seção temos que iniciar o do zero.
Passo 4
Agora vamos calcular a máxima tensão normal numa seção transversal em . Logo antes de o momento fletor vale e logo depois vale , assim vamos utilizar o segundo valor.
Agora é só substituir na equação da tensão normal:
Como a viga é uma viga a gente vai lá na tabela dos perfis de abas largas e acha os valores do momento de inércia e da altura:
Assim, podemos saber o valor de porque é a maior distância entre a linha neutra e superfície da peça. É basicamente a metade de :
E o momento de inércia :
Substituindo:
Passo 5
Por fim é só jogar na formulinha da tensão cisalhante, como a gente quer no ponto imediatamente a direita de vamos ter uma força cortante de:
Colocando na fórmula:
Da tabela de perfis de aba larga vamos ter que:
Assim podemos calcular a área:
Substituindo:
Resposta
a)
b)