Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 143
Duas placas de cobertura, cada uma com de espessura, são soldadas a uma viga de perfil laminado , como mostrado. Sabendo-se que , determinar: (a) a largura necessária das placas; (b) o comprimento necessário das placas.
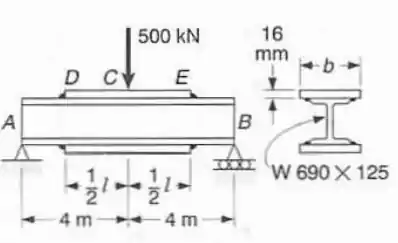
Passo 1
Fala aí, pessoal!!!
Para achar o comprimento nesse problema e achar a máxima tensão normal na seção a gente vai ter que calcular o módulo resistente da seção composta.
Depois disso a gente vai calcular o momento fletor no ponto centro da viga e através da seguinte relação vamos conseguir encontrar a nossa tensão:
Depois, para achar o comprimento a gente vai ter que descobrir qual o maior momento fletor que a viga sem a cobertura consegue aguentar, nesse ponto deverá começar o reforço!
Passo 2
Vamos achar o módulo resistente da seção , que é dado pelo momento de inércia dividido pela maior distância que se pode achar entre a linha neutra e a superfície.
Mas a gente tem que reparar que é uma figura composta, é o perfil mais as duas placas de cobertura. Se a gente for lá na tabela de perfis de abas largas vamos encontrar que o módulo de resistência desse perfil é:
Além disso vamos precisar também da altura da viga:
A gente pegou esses valores para que possamos calcular o módulo resistente da viga com as duas placas soldadas, como essas placas são retangulares podemos calcular o momento de inércia como:
Então para cada barra vamos ter:
Aplicando o teorema dos eixos paralelos podemos obter o momento de inércia da viga com as coberturas. Lembrando que o teorema dos eixos paralelos diz que:
Onde a área é a área de cada barra e a distância é a distância entre o centro da viga até o centro da barra:
Show! Esse é o momento de inércia da nossa viga composta. Agora para achar o módulo de resistência basta dividir por , sendo que é a distância do centro da viga até a superfície da barra:
Portanto, vamos ter:
Passo 3
Agora vamos calcular o momento fletor máximo que esta viga suporta. Para isso que tal fazermos um desenho simplificado dessa viga?
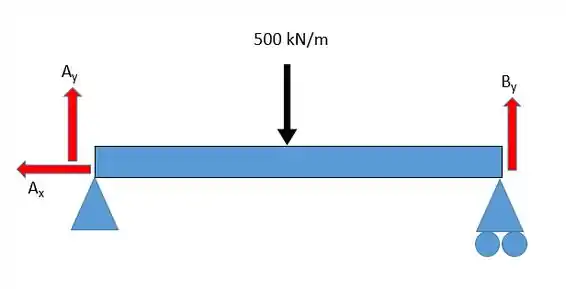
Já podemos perceber que a força é nula porque é a única força em . Agora vamos partir para o omatório das forças em :
Como a viga possui um carregamento simétrico então os termos e serão iguais:
Além disso, o momento fletor no ponto médio da barra será igual a:
Passo 4
Agora para calcular a máxima tensão normal a gente tem que lembrar que essa tensão máxima sempre ocorre no ponto mais superficial da viga, e é calculada como:
Substituindo os valores que achamos:
Passo 5
Para achar o comprimento vamos calcular o momento fletor num ponto da barra menor do que :
Agora vamos substituir esse valor na nossa equação.
Passo 6
Aqui é importante lembrarmos que a cobertura não existe, logo temos de utilizar o módulo resistente da viga sozinha, que é dado pela tabela:
Fazendo as substituições:
Lembre-se que não queremos queremos , podemos achar como:
Resposta
a)
b)