O pequeno rolo da haste esbelta uniforme repousa contra a superfície vertical em A enquanto a extremidade arredondada em B repousa sobre a plataforma que é lentamente girada para baixo começando da posição horizontal mostrada. Se a barra começar a deslizar quando = 25, determine o coeficiente de atrito estático entre a barra e a plataforma. Despreze o atrito no rolo e a pequena espessura da plataforma.

Passo 1
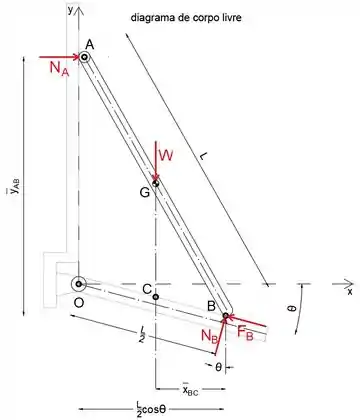
Primeiro, vamos isolar e desenhar o diagrama de corpo livre da haste AB
Podemos assumir com segurança que o ângulo será máximo quando a força de atrito FB for máxima
Conhecendo o coeficiente de atrito no ponto B, podemos escrever a força de atrito FB como

Passo 2
Ao igualar a soma das forças na direção y a zero, podemos escrever a força de reação NB como função do peso W
Podemos substituir FB por 0,40NB
Agora podemos expressar NB como
Ao igualar a soma das forças na direção x a zero, podemos escrever a força de reação NA como função do peso W
Primeiro, substituiremos o FB por 0,40NB
Passo 3
A seguir, vamos substituir NB pela expressão (2)
A partir daqui, podemos escrever NA como
Ao igualar a soma dos momentos sobre o ponto B a zero, também podemos escrever a força de reação NA como função do peso W
Podemos escrever NA como
Passo 4
Usando o teorema de Pitágoras, podemos determinar a distância vertical entre os pontos A e B
Embora usando a similaridade dos triângulos OBA e CBG e sabendo que G é o ponto médio da linha AB, podemos dizer que o ponto C é o ponto médio da linha OB, ou seja, que a distância horizontal entre os pontos B e C é
Podemos substituir e na expressão (4) pelas expressões (6) e (5), respectivamente
Passo 5
Observe que o ângulo máximo permitido é
uma vez que a parede irá impedir a rotação adicional da haste AB
Olhando para as equações (3) e (7), podemos notar que existem apenas duas incógnitas NA e nelas
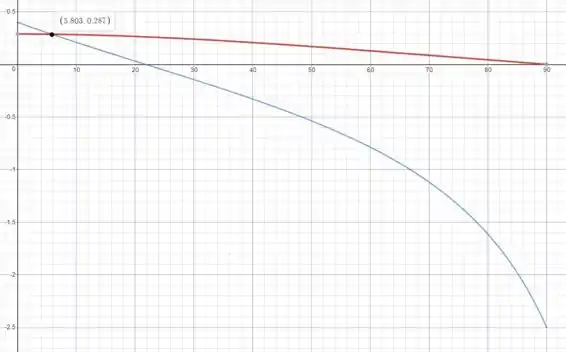
Usando uma calculadora gráfica como o Desmos (link nos comentários), representaremos as equações (3) e (7) no intervalo e leremos o ângulo que satisfaz ambas as equações do ponto de intersecção
Podemos ver que o ângulo em que o deslizamento começa é