Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 78
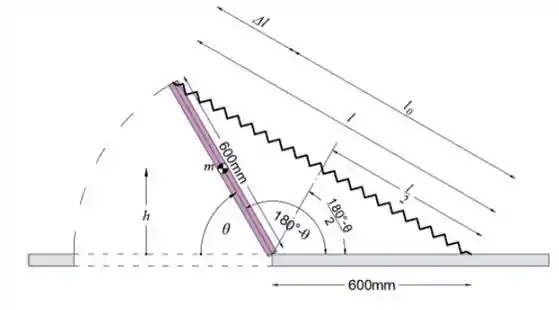
O alçapão uniforme de 25 kg é livremente articulado ao longo de sua borda inferior O-O e é preso às duas molas, cada uma com rigidez k = 800 N / m. As molas não são alongadas quando θ = 90 ∘. Tome V_g = 0 no plano horizontal através de O-O e plote a energia potencial V = Vg + Ve como uma função de θ de θ = 0 a θ = 90∘. Além disso, determine o ângulo θ para equilíbrio e determine a estabilidade desta posição.
Passo 1
Primeiro, vamos desenhar o diagrama de força ativa Observe que não há forças externas atuando no sistema, portanto, podemos escrever a equação de equilíbrio como
(1)
Podemos ver pelo esboço que metade do comprimento da mola é
Portanto, o comprimento total da mola é
Note que quando , a mola está relaxada, então o comprimento da mola é
Sabendo disso, podemos escrever a mudança no comprimento da mola como
Enquanto a altura do centro de massa é
Passo 2
Podemos escrever uma expressão para a energia potencial gravitacional como
substituiremos por e by
Derivaremos ambos lados das equações
(2)
Uma vez que temos duas molas acopladas, e escrevemos a mudança no comprimento da mola como Δl, podemos escrever a expressão para a energia potencial elástica como
Podemos substituir por e by
Derivaremos ambos lados da equação
Passo 3
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos a função para V = Ve + Vg no intervalo 0 ∘≤θ≤ 90
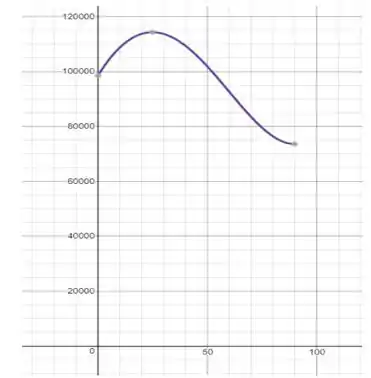
A seguir, substituiremos δVg e δVe pelas expressões (2) e (3) na equação (1)
Usando Desmos, podemos ver o ângulo θ que satisfaz a equação acima.
ou seja, em que o sistema está em equilíbrio é
Observe que, uma vez que a função está diminuindo em θ = 24,875 ∘, isso significa que a segunda derivada é menor que zero, ou seja, que o sistema é instável
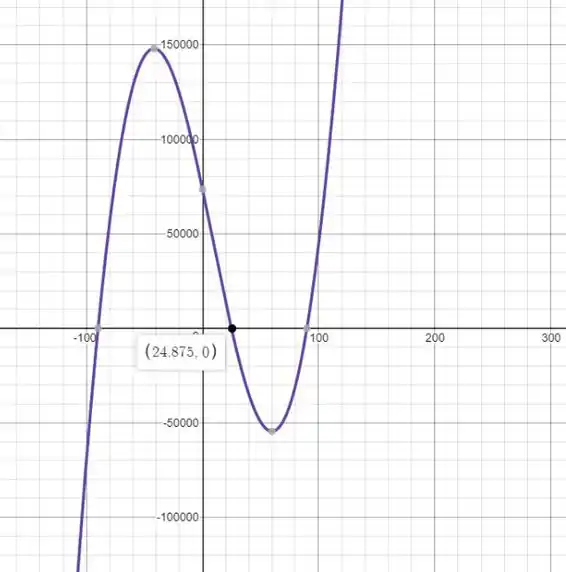
Resposta
o sistema é instável