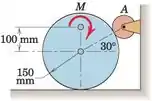
Sob a ação do engate M aplicado, o cilindro de 25 kg encosta no rolo A, que gira livremente. Se os coeficientes de atrito estático e cinético entre o cilindro e a superfície horizontal forem 0,50 e 0,40, respectivamente, determine a força de atrito F atuando no cilindro se (a) M = 20 N m e (b) M = 40 N m.
Passo 1
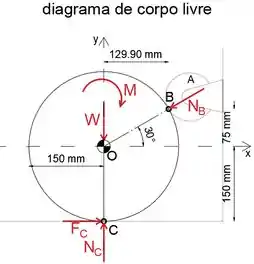
Primeiro, vamos desenhar o diagrama de corpo livre do cilindro
Vamos supor que o cilindro não está escorregando em C
Observe que, uma vez que o rolo A gira, portanto, há apenas a força de reação normal agindo em B
Peso do cilindro é
Passo 2
Ao igualar a soma dos momentos sobre o ponto C a zero, podemos determinar as forças de reação em B
Observe que já determinamos as distâncias entre o ponto B e o centro do cilindro usando um ângulo de 30 graus
Passo 3
Ao igualar a soma das forças na direção y a zero, podemos determinar a força de reação normal NC
Equacionando a soma dos momentos sobre o ponto O a zero, determinaremos a força de atrito FC
Passo 4
Devemos determinar a força de atrito máxima para ver se nossa suposição de que o cilindro não desliza em C está correta
Uma vez que a força de atrito FC calculada é menor que a força de atrito máxima, isso significa que o cilindro está parado, ou seja,
Passo 5
(b)
Desta vez, vamos supor que o cilindro está escorregando em C, portanto, podemos escrever a força de reação em C como
Ao igualar a soma das forças na direção x a zero, podemos determinar a força de reação NB
Podemos substituir FC por 0,40NC
Equacionando a soma das forças na direção y a zero, obtemos a equação com apenas uma incógnita, então podemos determinar a força de reação normal NC
Passo 6
Podemos substituir NB por 0,462NC
Uma vez que determinamos a força de reação NC, também podemos determinar a força FC
Finalmente, ao igualar a soma das forças sobre o ponto O a zero, determinaremos a força de atrito FC necessária para evitar o escorregamento
Passo 7
Podemos ver que a força de atrito de FC = 127,57 N não é suficiente para evitar o escorregamento, o que significa que nossa suposição estava correta, ou seja,