Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 65

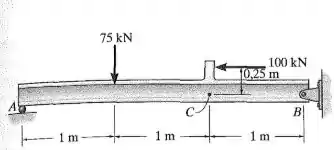
Se a viga ACB tiver seção transversal quadrada de 150   m m por 150   m m , determine a tensão de flexão máxima absoluta na viga.

Passo 1

Primeiro, vamos fazer o diagrama de momento para determinar o momento máximo. Vamos, então, determinar as reações:

∑ M a = 0 → - 75 × 1 + 100 × 0,25 + 3 B y = 0

B y = 16,67 k N

∑ F y = 0 → R a + 16,67 - 75 = 0

R a = 58,33 k N

∑ F x = 0 → B x - 100 = 0

B x = 100 k N

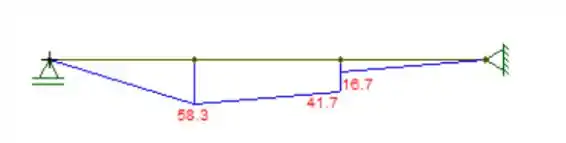
Com as reações, podemos fazer o diagrama:

Passo 2

O momento máximo vale 58,33kNm, logo:

σ m a x = 58033 × 1000 × 0,075 0,15 × 0,15 3 12 = 103,7 M P a

Resposta

σ m a x = 103,7 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga tem seção transversal retangular e está sujeita ao momento fletor M. Se o material de fabricação da viga tiver módulos de elasticidades diferentes para tração e compressão, como mostrado na fig
Determine as equações da linha elástica utilizando as coordenadas x1 e x2. EI é constante.
A viga é composta por duas hastes e está sujeita à carga concentrada P. Determine a deflexão máxima da viga, se os momentos de inércia das hastes forem IAB e IBC e o módulo de elasticidade for E.
A viga é composta por duas hastes e está sujeita à carga concentrada P. Determine a inclinação em C. Os momentos de inércia das hastes são IAB e IBC e o módulo de elasticidade é E.
Determine a equaçãoda linha elástica para a viga utilizando a coordenada x válida para 0 ≤ xL 2 . Especifique a inclinação em A e a deflexão máxima da viga. EI é constante.