Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 49
O projeto de uma viga reforçada de conreto é dito ser balanceado, se as máximas tensões no aço e no conreto são iguais às tensões admissíveis e respectivamente. Mostrar que para um projeto balanceado, a distância da superfície superior da viga até o eixo neutro é:
Onde e são os módulos de elasticidade do concreto e do aço, respectivamente e a distância da superfície superior da viga até os reforçadores de aço.
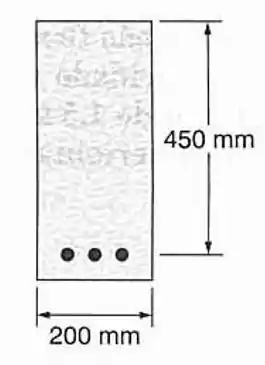
Passo 1
Agora estamos deparados com problema de “mostre que” então não tenhás medo JOVEM, esse problema é mais tranquilo do que parece.
Antes vamos ver como fica a seção transformada dessa figura de forma genérica, lembrando que o concreto não resiste à tração logo a parte de concreto que está abaixo da linha neutra é desprezada:
Passo 2
Agora vamos lembrar da equação que correlaciona a tensão e o momento fletor:
Onde:
- é a tensão normal admissível.
- é o momento fletor.
- o momento de inércia.
- a maior distância entre a linha neutra e um ponto da peça.
A tensão no concreto será:
Enquanto no aço:
Lembre-se do termo , que aparece quando utilizamos materiais diferentes.
Assim, podemos dividir uma pela outra e achar:
Como o termo é dado por:
Temos:
Isolando
Pronto!
Viu, acabou que essa questão envolve mais álgebra do que mecânica, de fato!
Resposta
Ei, a resposta está no passo a passo :)