Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 91
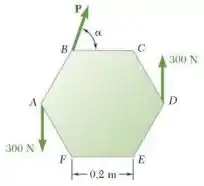
Uma placa hexagonal sofre a ação da força e do binário mostrados na figura. Determine a intensidade e a direção da menor força para a qual o sistema pode ser substituído por uma força única em .
Passo 1
Para este exercício, antes mesmo de dar início aos cálculos, alguns pontos podem ser analisados. Por exemplo, para que a força seja mínima em relação ao ponto de interesse , ela deve estar perpendicular ao vetor posição que liga o ponto ao ponto (o ponto de interesse e o ponto de atuação da força, respectivamente). Logo, sabemos que o ângulo pode ser determinado observando o esquema:
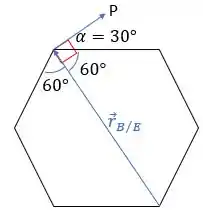
Como cada ângulo interno ao hexágono forma , o vetor posição divide-o em dois ângulos de , tal que para que esteja perpendicular a esse vetor, deve ser .
Passo 2
Agora, para substituir o sistema por apenas uma força equivalente no ponto deve ser eliminado o efeito do binário presente. Isso pode ser feito através do somatório de momentos visto que o momento gerado pela força deve ter a mesma magnitude do momento binário.
Logo, aplicando o equilíbrio de momentos em relação a tem-se:
Lembrando que o momento binário é dado por:
onde é a distância perpendicular entre as linhas de ação das forças que geram o binário, então:
O valor de pode ser encontrado por:
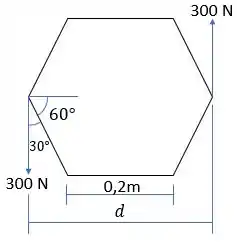
Assim,
Passo 3
Com esses valores encontrados, se torna possível determinar o valor de . Portanto: