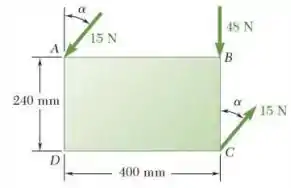
Uma placa retangular sofre a ação da força e do binário mostrados na figura. Esse sistema deve ser substituído por uma força única equivalente. Especifique o valor de sabendo que a linha de ação da força equivalente intercepta a linha à direita de .
Passo 1
Observando os dados que o exercício dá, pode-se montar o seguinte esquema:
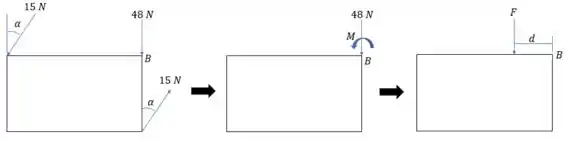
Onde agora tem o valor de .
Passo 2
Para realizar a eliminação do binário existente no sistema, sabe-se que o momento gerado pela força equivalente deve se igualar ao momento gerado pelo binário. Logo, isso demonstra que ao fazer o somatório de momentos em relação ao ponto , podemos escrever:
Ou seja:
Passo 3
Uma estratégia para se determinar o valor de é utilizar razões trigonométricos para deixar a equação em função de apenas uma função trigonométrica. No caso presente, o ideal seria deixar toda a equação em função de seno ou cosseno. Para tanto, rearranjando a equação de modo a facilitar os próximos cálculos:
Então, elevando ao quadrado a equação, tem-se:
Lembrando da razão trigonométrica:
ou ainda,
E substituindo na equação original, obtém-se:
Que pode ser reescrita como:
Passo 4
Aplicando a fórmula de Bhaskara:
E encontra-se os dois valores para :
Respectivamente, eles dão os resultados:
Ou
Resposta
Ou