Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 92a
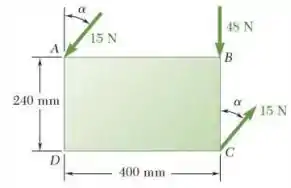
Uma placa retangular sofre a ação da força e do binário mostrados na figura. Esse sistema deve ser substituído por uma força única equivalente. Para , especifique a intensidade e a linha de ação da força equivalente.
Passo 1
Para substituir o sistema por apenas uma força equivalente no ponto deve ser eliminado o efeito do binário presente. Isso pode ser feito através do somatório de momentos visto que o momento gerado pela força de deve ter a mesma magnitude do momento binário.
Logo, aplicando o equilíbrio de momentos em relação a tem-se:
Para a parte deste exercício, o valor do ângulo é de . Logo:
Passo 2
Agora, com o momento resultante no ponto e a força de agindo no mesmo ponto, esse conjunto momento-força pode ser substituído por uma única força a uma certa distância de . Isso possibilita a eliminação do binário presente no sistema como mostra o esquema a seguir:
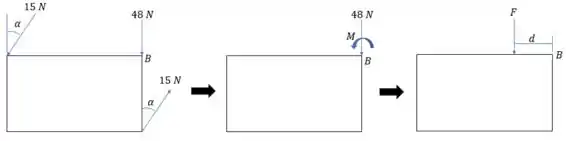
Para este caso, a força equivalente terá a mesma intensidade da força em , mas estará a uma certa distância do mesmo para gerar um momento que se iguale ao momento binário a fim de eliminá-lo. Dessa forma:
Resposta
com a sua linha de ação interceptando perpendicularmenete o lado do retângulo a uma distância do ponto .