Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 36

Uma barra leve AD é suspensa pelo cabo BE e suporta um bloco de 200 N em C. As extremidades A e D da barra estão em contato, sem atrito, com as paredes. Determine a tração no cabo BE e as reações em A e D.

Passo 1

Tá legal, vamos lá! A primeira coisa que fazemos nesse tipo de exercício é desenhar o DCL do sistema:

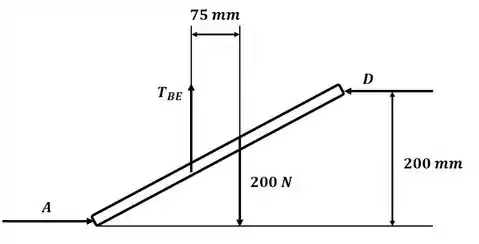
Ok! Agora, para descobrir o valor da força de tração , vamos aplicar o somatório de forças na direção :

Isolando e resolvendo, temos:

Passo 2

Agora, aplicando o somatório de forças na direção :

Passo 3

Agora, analisando o DCL do passo 1, podemos ver que os dois pares de forças, na horizontal e na vertical, formam dois momentos de binário, dessa forma, podemos aplicar o somatório de momento para o sistema para obter o valor de e consequentemente de , já que vimos que são iguais:

Isolando A e resolvendo, temos:

E, como vimos no passo 2, , então:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força horizontal P de 80 N é aplicada no ponto A de um elemento estrutural. Substitua P por um sistema força-binário equivalente em B e um sistema equivalente que consista em uma força vertical em

Resolva o Problema 3.151 quando a tensão no cabo A B é 1.360 N .

Uma cablagem é feita pela passagem de dois ou três fios em torno de cavilhas de diâmetro 50m m montadas em uma placa de compensado de madeira. Se a força de cada fio é 12N , determine o binário result

As cordas A B e B C são duas das cordas usadas para suportar uma barraca. As cordas estão fixadas a uma estaca em B . Se a tensão na corda A B é 540N , determine a o ângulo entre a corda A B e a estac

Um fazendeiro utiliza cabos e guinchos B e E para aprumar uma lateral de um pequeno celeiro. Sabendo que a soma dos momentos em relação ao eixo x das forças exercidas pelos cabos sobre o celeiro nos p