Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 102
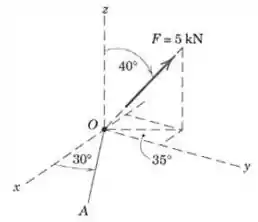
Expresse como um vetor em termos dos vetores unitários , e . Determine a projeção de , tanto como um escalar quanto como um vetor, sobre a linha , que está situada no plano -.
Passo 1
Começamos tentando escrever em termos dos vetores unitários. Podemos fazer isso procurando cada uma das componentes através dos ângulos que foram dados na figura do enunciado:
Para projetar o vetor nos eixos e , precisamos seguir dos passos: primeiro projetá-lo no plano , e só então projetar em cada eixo:
E então o vetor fica da seguinte forma:
Passo 2
Agora vamos pensar na projeção de sobre a linha , para isso precisamos definir algum vetor na direção dessa linha.
(Que já é um vetor unitário). Para encontrar a projeção de sobre como um escalar precisamos usar o produto escalar:
Vamos chamar esse escalar de , já que é a projeção da força sobre a linha :
Passo 3
Para encontrar a projeção de sobre como vetor é só multiplicar o escalar que acabamos de calcular pelo vetor unitário na direção de :
Resposta
, e as projeções são e .