Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 114
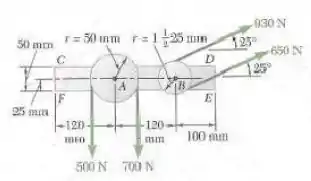
As polias e estão montadas sobre o suporte . A tração em cada lado das duas correias é mostrada na figura. Substitua as quatro forças por uma força única equivalente e determine em que ponto a sua linha de ação intercepta a parte inferior do suporte.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar a força equivalente que atua sobre o sistema, ou seja, vamos somar todas as forças atuantes e ver qual a resultante.
Vamos analisar as forças que agem em . Temos que:
Analisando o momento que essas forças geram, temos:
Faremos o mesmo com o ponto :
Analisando o momento que essas forças geram, temos:
Passo 2
Agora teremos o seguinte arranjo:
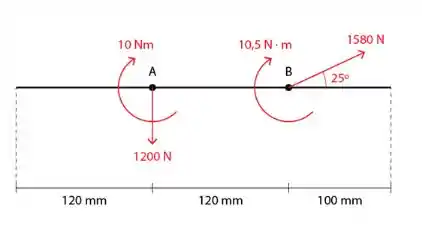
Analisando o diagrama podemos fazer o somatório das forças. Analisando as forças horizontais, temos que:
indica a resultante das forças horizontais que agem no sistema.
Faremos agora o somatório de forças em verticais, temos que:
indica a resultante das forças verticais que agem no sistema. Observe que o sinal foi negativo, o que indica que a direção da resultante é para o lado baixo.
Passo 3
Como temos a resultante vertical e horizontal, podemos obter a reação resultante a partir do teorema de Pitágoras. O arranjo das reações ficou assim:
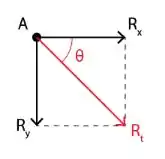
Calculando a resultante, temos:
Substituindo os valores, temos:
Passo 4
Como temos o momento gerado pleas forças e binários, podemos calcular a distância em que a linha da força intercepta o segmento .
Portanto a linha de ação da força passa a à direita do ponto .