Para a estrutura e carregamento mostrados na figura, determine as reações e quando (a) e (b) .
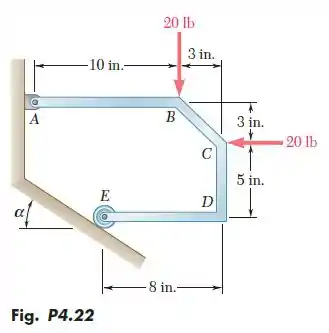
Passo 1
Bom galera, o segredo da questão é notar que o corpo está em equilíbrio, então o somatório dos momentos é nulo. Para fazer o somatório dos momentos no ponto A, vamos começar decomponto a reação de apoio no ponto E.
A reação em E é perpendicular ao plano em que a rodinha está apoiada, ou seja, ela faz um ângulo com a vertical. Então as componentes vão ser:
Então, no ponto A, temos:
Com isso, a gente já consegue achar uma expressão pra calcular a reação E, em função do ângulo:
Já as reações em A a gente pode achar fazendo o somatório de forças verticais e horizontais:
Logo:
Pessoal, foi bom a gente ter resolvido o exercício de forma assim literal, em função de alpha, porque agora a gente já tem essas expressões prontas pros itens a e b. E é só substituir o valor do ângulo.
Passo 2
Para o item a,
Passo 3
Para o item a,
Resposta
Quando
Quando