Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 156
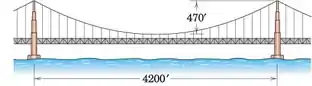
A ponte Golden Gate em São Francisco tem um vão principal de 4200 pés, uma curvatura de 470 pés e uma carga estática total de 21.300 lb por pé linear de medição horizontal. O peso de ambos os cabos principais está incluído nesta figura e presume-se que esteja uniformemente distribuído ao longo da horizontal. O ângulo formado pelo cabo com a horizontal no topo da torre é o mesmo em cada lado de cada torre. Calcule a tensão midspan T0 em cada um dos cabos principais e a força compressiva C exercida por cada cabo no topo de cada torre.
Passo 1
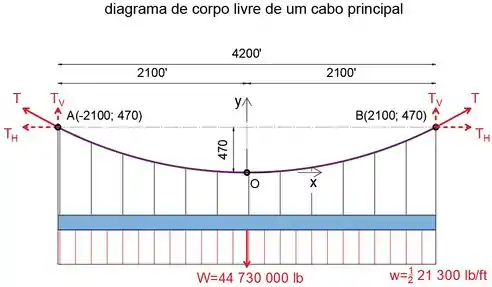
Primeiro, vamos desenhar o diagrama de corpo livre de um cabo principal. Observe que, devido à simetria, ambos os cabos suportam o mesmo peso, portanto, o peso por comprimento suportado por um cabo principal é:
E o peso total suportado por um cabo é:
Observe que no midspan o cabo é horizontal, portanto, a tensão que atua no midspan tem apenas componente horizontal.
Passo 2
Ao aplicarmos a lei de ação e reação, podemos ver que a força compressiva atuando na torre eadh por um cabo é igual à componente vertical da tensão T
Passo 3
Ao igualar a soma das forças na direção y a zero, podemos determinar a força Cv
Uma vez que o componente horizontal da força atuando no cabo é marcado como CH, a função do cabo parabólico é:
Passo 4
Colocando as coordenadas do ponto B e o valor da carga distribuída w na equação (5/14), podemos determinar a componente horizontal da tensão (CH)
Finalmente, substitua TV e TH por seus valores nas expressões (1) e (2)