Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 48
A treliça é composta de sete membros, cada um tendo uma massa por unidade de comprimento de . Localize a posição do centro de massa. Despreze a massa das placas de ligação nas juntas.
Passo 1
Fala ai galerinha bonita, tudo beleza?
Saca só, o enunciado nos deu um sistema de treliças como na figura abaixo:
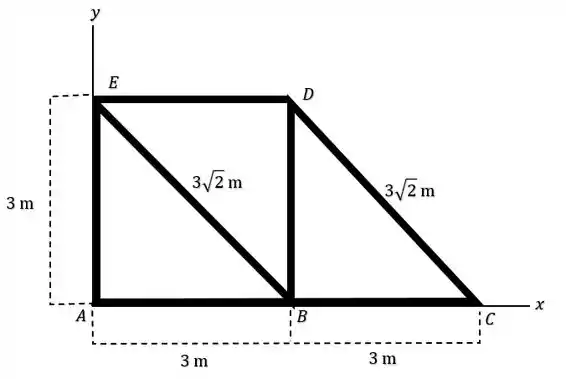
E sabendo que a treliça possui uma massa por unidade de comprimento de , o enunciado quer que a gente localize a posição do centro de massa!
Nesse caso, como o centro de massa coincide com o centro de gravidade e com o centroide, podemos dividir o sistema em membros e usar as equações:
E com elas vamos conseguir encontrar o centro de massa da treliça.
Passo 2
Iradoso, então se a gente montar uma tabelinha com os centroides de cada membro, e o valor de e , vamos obter que:
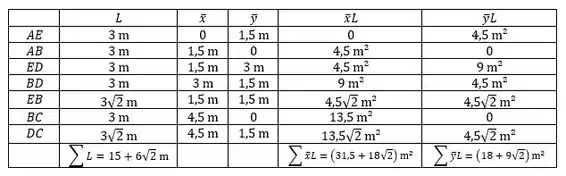
Então para a componente do centro de massa, teremos:
Logo:
E para o eixo :
Tal que:
Portanto, o centro de massa da treliça composto vai estar na coordenada;