Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 108
Uma ponte rolante para transportar tambores de aço de 135 kg é mostrada. Calcule o módulo da força exercida no tambor em e .
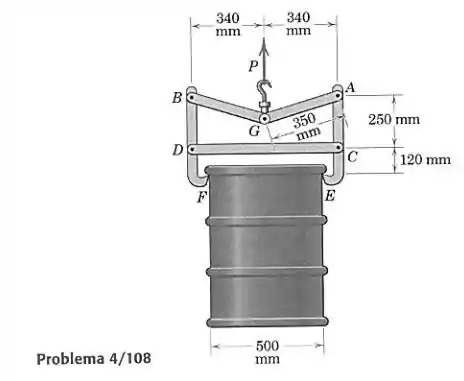
Passo 1
Pela simetria, as forças são iguais em e , então só calcularemos para um lado. Se olharmos para a barra lateral , vemos que as forças que atuam nela são as reações em ( e ), a força feita pelo elemento e a força feita por . Como temos 4 incógnitas, não conseguimos resolver só com as equações desse elemento. Vamos então primeiro calcular através do equilíbrio no ponto . Pela simetria . Vamos lá:
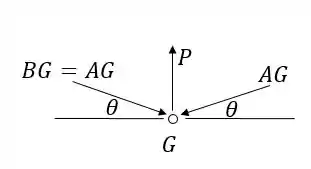
Primeiro calculamos a força :
Agora devemos saber o seno do ângulo . A distância horizontal entre e (cateto adjacente) é 340 mm, e a distância entre os dois pontos (hipotenusa) vale 350 mm, então:
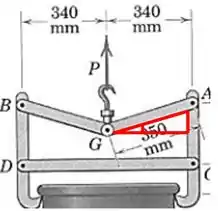
Agora achamos pela relação fundamental:
Então:
Passo 2
Já temos então vamos olhar para o elemento :
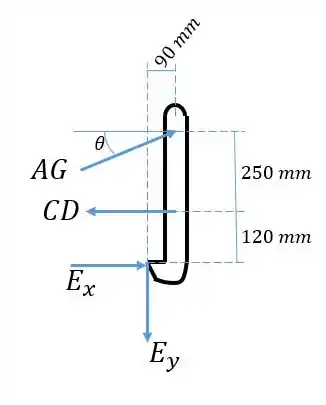
Primeiro achamos diretamente com a soma das forças em :
Fazendo o momento em torno de , encontramos :
Agora achamos fazendo a soma das forças em :
Passo 3
Pronto, já temos as componentes de agora só precisamos calcular seu módulo:
Como , temos também: