Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 54
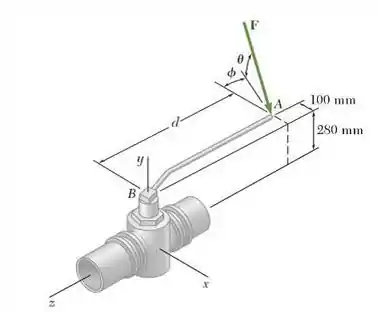
54. Durante a aplicação da froça na alavanca da válvula mostrada na figura, os seus momentos sobre os eixos e são, respectivamente e . Para , determine o momento de sobre o eixo .
Passo 1
Bom! Antes de mais nada, vamos definir a expressão de momento em relação a origem como sendo:
Em seguida, a segunda coisa que temos que fazer é determinar a distância em termos dos vetores unitários e ; afinal esse segmento é o vetor posição . Para isso, basta observar a figura do enunciado. O enunciado nos diz que . Veremos que o ponto está nas coordenadas em milímetros e o ponto, que é a nossa origem, encontra-se nas coordenadas . Com isso, para achar basta fazer a diferença entre as coordenadas de e as coordenadas de :
Passo 2
Achada o nosso vetor , vem aí a parte mais difícil. Olha só a figura, mais uma vez:
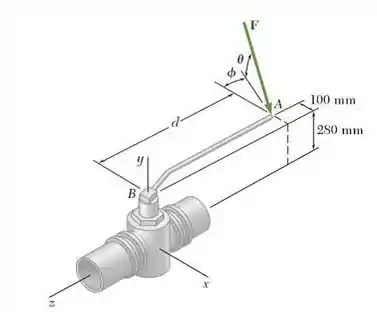
A força faz um ângulo com o plano horizontal e depois um ângulo com aquela retazinha que está na figura. Isso quer dizer que teremos que decompor duas vezes para encontrar as coordenadas em termos de e . Façamos isso:
E como :
Passo 3
A questão já nos fornece os momentos em relação aos eixos e provenientes da força exercida . Ora bolas; tudo que temos que fazer agora é relacionar esses momento já fornecidos com a expressão geral do momento que queremos encontrar, especificamente para os eixos e .
Apliquemos a definição de momento:
Onde temos que:
Vamos então, fazer o produto vetorial usando o determinante matricial:
E disso, tiramos que:
E como sabemos que , e , vamos tratar de determinar se podemos tirar alguma relação entre e .
Utilizaremos primeiro :
E depois, trabalhando com :
Agora, vamos substituir essa relações anteriores na fórmula do :