Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.10 - Ex. 118
Um dispositivo de travamento por atrito permite que a barra se mova para a esquerda, mas previne movimento para a direita. Se o coeficiente de atrito entre a sapata e a barra vale 0,40, especifique o máximo comprimento do braço de ligação que permitirá que o dispositivo trabalhe como descrito.
Passo 1
Se uma força é aplicada na barra e a barra está em equilíbrio, essa força será transmitida à sapata. Então representamos em diagrama de corpo livre a sapata. Além da força de atrito , temos também a força normal aplicada no mesmo ponto, e a força feita pelo braço de ligação, que tem ângulo em função do valor de .
Passo 2
Como podemos ver no desenho, pelo equilíbrio a resultante causada pela barra na sapata deve obrigatoriamente ter mesmo módulo e direção do braço. Mas sabe-se que a angulação em relação à linha normal à superfície deve ser o ângulo , dado por:
Sendo coeficiente de atrito entre as superfícies. Então:
Esse ângulo pode ser visto na imagem, em um triângulo que tem como hipotenusa:
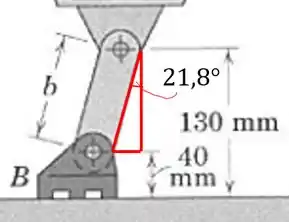
Então achamos através do cosseno do ângulo: