Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 187
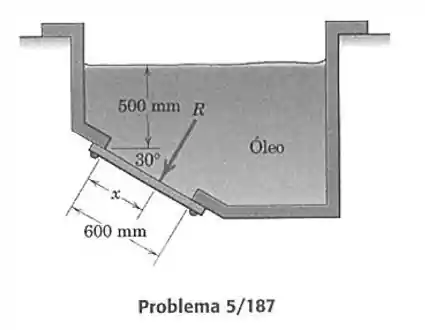
187- Uma seção vertical de um tanque para drenagem do óleo está mostrada. A placa de acesso cobre uma abertura retangular, que tem uma dimensão de normal ao plano do papel. Calcule a força total exercida pelo óleo sobre a placa e a localização de . O óleo tem uma massa específica de .
Passo 1
No começo da placa de acesso a placa sofre um pressão e no final dessa placa ela sofre uma pressão maior do que já que ela está mais profunda, isso nos dá um sistema de forças igual a:
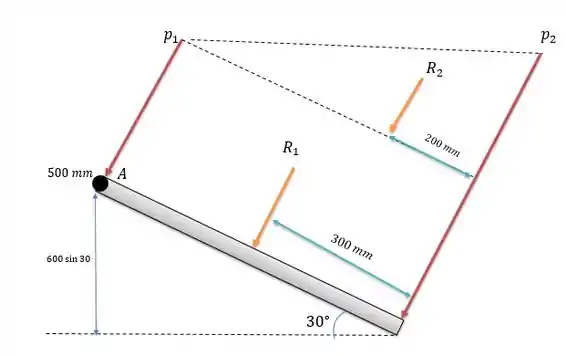
A pressão vale:
E a pressão vale:
Passo 2
Logo a força valerá:
Pois como a pressão é constante.
E :
Onde temos que utilizar a pressão média presente no triângulo formado:
Passo 3
A força resultante total será a soma de com :
O momento que a resultante faz na placa é a mesma que as duas forças fazem em .
Considerando que a força resultante está em na placa, logo: