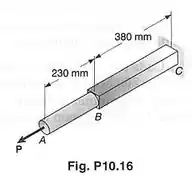
Uma porção de uma barra de aço quadrada, de de lado, foi usinada produzindo um cilindro de diâmetro , como mostrado. Sabendo-se que a tensão normal admissível do aço é e , determinar, para o carregamento mostrado, a máxima energia de deformação que pode ser acumulada pela barra .

Faaaala, meus queridos! Prontos para uma questão de energia de deformação?

O enunciado quer que a gente calcule a máxima energia de deformação de uma barra sob carga . A barra é formada por duas barras: (barra quadrada) e (cilindro). A barra possui área de seção transversal constante igual a e lado . A barra possui área de seção transversal constante igual a e diâmetro .

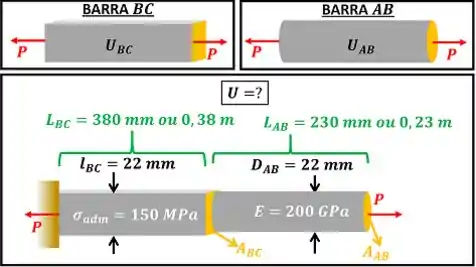
e são as energias de deformação das barras e respectivamente. e são os comprimentos das barras e respectivamente.

Como precisamos calcular a máxima energia de deformação , a força que age sobre a barra deve ser a parior força possível! Logo, é a máxima tensão vezes a área .

Mas por que usamos a área e não a área ?

Porque a área é menor que a área . Temos que usar a menor área, porque as menores áreas geram as maiores tensões! Logo, a menor área alcança a tensão limite para menores cargas .

Como podemos ver na figura acima, a barra é a soma das barras e . Por causa disso, a energia de deformação da barra total tem que ser igual à soma entre a energia de deformação da barra mais grossa e a energia de deformação da barra mais fina.

A fórmula que calcula as energias de deformação de barras com áreas da seção transversal constantes é a fórmula 10.14 do livro.

Usaremos essa fórmula para e .

onde é o módulo de elasticidade que vale segundo o enunciado.

Agora que temos todas essas informações em mãos, vamos calcular a energia de deformação da barra toda nos próximos passos!