Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 19
A barra é feita de aço ára o qual e . Sabendo-se que uma energia de deformação de deve ser acumulada pela barra assim que a carga axial é aplicada, determinar o coeficiente de segurança da barra em relação a deformação permanente, quando .
Passo 1
E aííí, galera bonita! Estão com ânimo para fazer uma questão de energia de deformação?
O enunciado quer que a gente calcule o coeficiente de segurança que evita a barra de se deformar permanentemente. Esse coeficiente é igual à energia máxima que a barra atinge antes de se deformar permanentemente dividida pela energia que a barra tem, quando está sob carga .
Nós já temos . Logo, para calcular precisamos achar apenas .
A imagem abaixo mostra a barra em pé com os dados que precisamos para achar .
Note que a barra é formada por duas barras: (mais grossa) e (mais fina). A barra mais grossa possui área de seção transversal constante igual a e diâmetro . A barra mais fina possui área de seção transversal constante igual a e diâmetro .
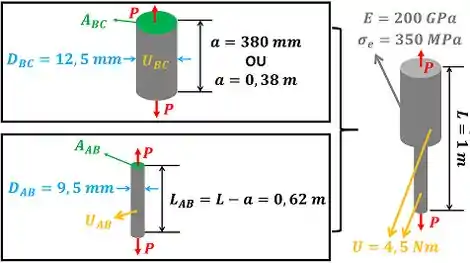
é o módulo de elasticidade da barra. é o comprimento da barra. é o comprimento da parte grossa da barra (barra ). é a máxima tensão que a barra pode sofrer sem se deformar permanentemente. e são as energias de deformação das barras e respectivamente. Como a barra é formada por essas duas barras, a energia é a soma de e .
No entanto, para achar as energias e que as partes da barra têm quando a barra está prestes a se deformar permanentemente, precisamos achar a carga que causa essa deformação permanente. Essa carga é igual à tensão vezes .
Mas por que usamos a área e não a área ?
Porque a área é menor que a área . Temos que usar a menor área, porque as menores áreas geram as maiores tensões! Logo, a menor área alcança a tensão limite para menores cargas .
Agora que sabemos de tudo isso, podemos descobrir como achar as energias e através da carga no próximo passo!
Passo 2
Nesse passo, a gente vai encontrar as energias e .
A fórmula que calcula as energias de deformação de barras com áreas da seção transversal constantes é a fórmula 10.14 do livro. Como e têm áreas constantes:
Ou seja, para calcular e , temos que achar e em .
Primeira etapa cumprida! Vamos achar a força agora!
Mas antes, temos que lembrar que a tensão admissível vale .
Por fim, temos que converter de para , multiplicando por .
Substituindo tudo isso na fórmula de e , achamos:
Agora podemos achar e o coeficiente de segurança .
Passo 3
Nesse passo, a gente vai calcular o valor da energia máxima que a barra tem antes de se deformar permanentemente e o valor do coeficiente de segurança .
Começamos por :
Substituindo esse valor na fórmula de , achamos:
Aeeeeeeee! Fechamos outro exercício! Tá ficando expert, heim?