Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 139

Resolver o prob. 10.138 assumindo que a carga P é deslocada ao longo da sua linha de ação e aplicada no ponto C.

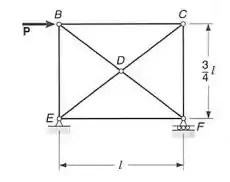
Passo 1

Corte membro AB no final A e substitua força membro F A B   pela carga F A ← atuando no membro A B no final A.

δ A = δ U δ F A = δ δ F A Σ F 2 L E A = 1 E A Σ   F δ F δ F A   L = 0

Passo 2

Junta B + → Σ F X = 0                         - F A - 4 5 F B D = 0                   F B D = - 5 4 F A

+ ↑ Σ F y = 0             - P - F B E - 3 5 F B D = 0       F B E = - P + 3 4 F A

Passo 3

Junta C + ↑ Σ F y = 0             F B E + 3 5 F A E = 0                 F A B E = 5 3 P ` - 5 4 F A

+ → Σ F x = 0           - 4 5 F A E = F D E = 0                 F D E = - 4 3 P + F A

Resposta

4 3 P + F A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada elemento da treliça mostrada é feito de aço e tem uma área de seção transversal de 400m m 2 . Usando E = 200G P a , determine a deflexão (o deslocamento) no ponto D causado pela carga de 16k N .
O navio em A começou a perfurar um poço de petróleo no fundo do oceano a uma profundidade de 1524m . A broca de perfuração de aço em forma de tubo tem um diâmetro externo de 203,2m m e uma espessura d
A haste A B é feita de aço para o qual a tensão de escoamento é σ E = 450M P a e E = 200G P a ; a haste B C é feita de uma liga de alumínio para a qual σ E = 280M P a e E = 73G P a . Determine a máxim
Um bloco de peso W é colocado em contato com uma viga em um certo ponto D e liberado. Mostre que a deflexão máxima resultante no ponto D é duas vezes maior do que a deflexão provocada por uma força es
Cada elemento da treliça é mostrada é feito de aço e tem uma área de seção transversal conforme apontado. Usando E = 29 × 10 6p s i , determine a energia de deformação .