Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 178a

A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a maior tensão de compressão quando (a) a = 0 (b) a = 30   m m

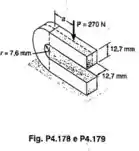
Passo 1

A região que sofre maior esforço é o centro da curva. Então vamos fazer uma seção neste ponto e calcular os esforços internos

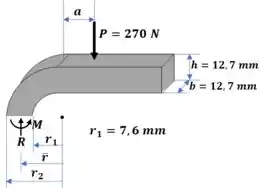
Primeiro vamos calcular as propriedades geométricas da seção: raio do centroide, raio externo e área:

r - = r 1 + h 2 = 7,6 + 12,7 2 = 13,95   m m

r 2 = r 1 + h = 20,3   m m

A = h ⋅ b = 12,7 ⋅ 12,7 = 161,29   m m 2

Passo 2

Com o raio podemos calcular o momento interno, já que a distância entre a força P e o centro da viga é ( a + r - )

M = P a + r - = 270   N   ( a + 13,95   m m )

E a carga interna R será igual a carga P :

R = P = 270   N

Passo 3

Como a seção é quadrada, a gente calcula o raio da linha neutra pela equação:

R = h ln ⁡ r 2 r 1 = 12,7 ln ⁡ 20,3 7,6 = 12,9266   m m

E com isso, a gente calcula a excentricidade:

e = r - - R = 1,0234   m m

Passo 4

Cuidado! Um erro comum nesse tipo de questão é esquecer de calcular a tensão gerada pela força interna R:

σ R = R A

Não esqueça de que é uma compressão! Ou seja, a tensão é negativa:

σ R = - 270   N 161,29   m m 2

σ R = - 1,674   M P a

Passo 5

Beleza!

Agora a tensão real sobre viga vai ser a soma da tensão σ R mais a tensão gerada pelo momento

Para o caso de a = 0 :

M = 270   N   a + 13,95   m m = 3766,5   N ⋅ m m

A tensão no raio interno:

σ r 1 = σ R + M ⋅ r 1 - R A e r 1

σ r 1 = - 1,674   M P a + 3766,5   N ⋅ m m ⋅ ( 7,6   m m - 12,9266   m m ) 161,29   m m 2 ⋅ 1,0234   m m ⋅ 7,6   m m

σ r 1 = - 1,674   M P a - 15,993   M P a

σ r 1 = - 17,667   M P a

A tensão no raio externo:

σ r 2 = σ R + M ⋅ r 2 - R A e r 2

σ r 2 = - 1,674   M P a + 3766,5   N ⋅ m m ⋅ ( 20,3   m m - 12,9266   m m ) 161,29   m m 2 ⋅ 1,0234   m m ⋅ 20,3   m m

σ r 2 = - 1,674   M P a + 8,288   M P a

σ r 2 = 6,614   M P a

Resposta

σ r 1 = - 17,667   M P a

σ r 2 = 6,614   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de mesas largas com o carregamento mostrado, determine a maior carga P que pode ser aplicada, sabendo-se que a tensão normal máxima é de 24 ksi e a maior tensão de cisalhamento usando a ap
Para a viga e o carregamento mostrado, considere a seção n-n e determinar (a) a maior tensão de cisalhamento em nessa seção, (b) a tensão de cisalhamento no ponto a.
Determine a tensão máxima em cada um dos elementos de máquina mostrados.
A parte curva da barra mostrada na figura tem um raio interno de 20m m . Sabendo que a tensão admissível na barra é de 150M P a , determine a maior distância possível da linha de ação da força de 3k N
A parte vertical da prensa mostrada na figura consiste em um tubo retangular com espessura de parede t = 10m m . Sabendo que a prensa foi usada para prender blocos de madeira que estavam sendo colados