Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas de Revisão - Ex. 90

Para a viga e o carregamento mostrado, considere a seção n-n e determinar (a) a maior tensão de cisalhamento em nessa seção, (b) a tensão de cisalhamento no ponto a.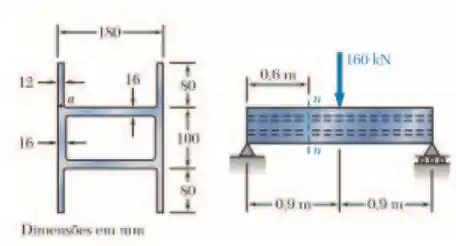

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente a tensão de cisalhamento em (a) ponto a, (b) ponto b.

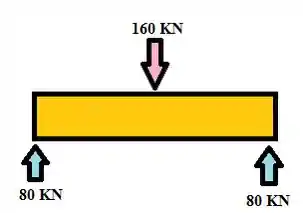
As reações que temos são dos mesmos valores

R A = R B = 80   K N

Passo 2

Entao teremos agora que determinar a inércia total do elemento, mas precisamos fazer por partes, vem comigo ;D

I 1 = 1 12 x 12 x 80 3 + 12 x 80 x 90 2 = 8,28 x 10 6 m m 4

I 2 = 1 12 x 1 80 x 16 3 + 1 80 x 16 x 42 2 = 5,14 x 10 6 m m 4

I 3 = 1 12 x 1 6 x 68 3 = 419,24   x 10 3 m m 4

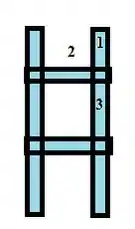
Agora a inércia total vem comigo ;)

I = 4 x 8,28 x 10 6 + 2 x 5,14 x 10 6 + 2 x 419,24   x 10 3 = 44,27   x   10 6 m m 4 = 44,27   x   10 - 6 m m 4

Passo 3

Agora podemos calcular Q da linha neutra das seções pré definidas anteriormente:

Q 1 = 12 x 70 x 90 = 86,4 x 10 3   m m 4

Q 2 = 1 80 x 16 x 42 = 120,96   x 10 3   m m 4

Q 3 = 16 x 34 x 17 = 9,248   x 10 3   m m 4

Agora Q total vem comigo ;)

Q = 2 x 86,4 x 10 3   + 120,96   x 10 3   + 2 x 9,248   x 10 3   = 312,256 x 10 3   m m 4 = 312,256 x 10 - 6   m m 4

Agora sim podemos determinar a tensão de cisalhamento;

τ = V Q I t = 80 x 10 3 x 312,256 x 10 - 6   44,27   x   10 - 6 x 12 x 10 - 3 = 17,63 x 10 6 P a

Passo 4

No ponto a.

Q = Q 1 = 86,4 x 10 3   m m 4 = 86,4 x 10 - 6   m 4

τ = V Q I t = 80 x 10 3 x   86,4 x 10 - 6   44,27   x   10 - 6 x 12 x 10 - 3 = 13,01   x 10 6   P a

Resposta

  1. 17,63 x 10 6 P a
  2. 13,01   x 10 6   P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o P r o b l e m a4.121 considerando que as deformações medidas são: ε A = + 600μ eε B = + 420μ
Uma coluna curta em perfil laminada de aço suporta uma placa rígida na qual duas ações PeQ são aplicadas conforme mostrado. As deformações foram medidas nos dois pontos AeB na linha de centro da face
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
O momento M é aplicado a uma viga com a seção transversal mostrada na figura em um plano formando um ângulo β com a vertical. Determine a tensão no.Ponto A;Ponto B;Ponto D.
Uma única força vertical P é aplicada a um poste curto de aço conforme mostrado. Extensômetro localizados em A, B e C indicam as seguintes deformações: ε A = - 500μ eε B = - 1000μ eε C = - 200μ Sabend