Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 77
Uma porção de fêmur pode ser modelada como um tubo com diâmetro interno de e diâmetro externo de . Determine a força estática elástica máxima P que pode ser aplicada ao centro do osso sem causar fratura. Considere que as extremidades do osso estão apoiadas em roletes. O diagrama para a massa do osso é mostrada na figura e é o mesmo para tração e para compressão.
Passo 1
Fala! Para achar a força elástica máxima, vamos precisar usar a expressão para a tensão máxima, e para isso precisamos do momento máximo nesse osso aí.
Mas não se assusta com essa questão do osso, não. Essa situação que ele descreveu pode ser entendida como uma viga biapoiada com uma carga concentrada no meio, saca?
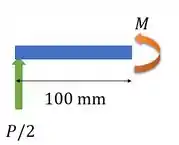
Para esse tipo de situação, a gente pode lembrar que o momento máximo ocorre no meio da viga. E que por simetria, as reações nos apoios serão . Vamos calcular esse momento:
Passo 2
Temos essa situação:
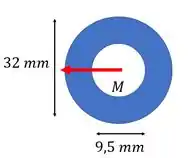
O momento de inércia fica:
Passo 3
A força elástica acontece no regime elástico. Que é o primeiro intervalo onde o gráfico fica linear. O valor máximo da tensão nesse intervalo é a nossa tensão máxima:
Como a tensão causada pelo momento é dada por:
E como a tensão máxima é causada no mais distante do eixo onde o momento está sendo aplicado, ou seja, em .
E como , podemos determinar P: